13 câu hỏi trắc nghiệm thuộc Tổng hợp đề thi chính thức vào 10 môn Toán năm 2019 có đáp án (Phần 1)- Đề 27

Tổng hợp đề thi chính thức vào 10 môn Toán năm 2019 có đáp án (Phần 1)

Đề số 1
Đề số 2
Đề số 3
Đề số 4
Đề số 5
Đề số 6
Đề số 7
Đề số 8
Đề số 9
Đề số 10
Đề số 11
Đề số 12
Đề số 13
Đề số 14
Đề số 15
Đề số 16
Đề số 17
Đề số 18
Đề số 19
Đề số 20
Đề số 21
Đề số 22
Đề số 23
Đề số 24
Đề số 25
Đề số 26
Đề số 27
Đề số 28
Đề số 29
Đề số 30

Tổng hợp đề thi chính thức vào 10 môn Toán năm 2019 có đáp án (Phần 1)- Đề 27

6695 lượt thi
13 câu hỏi
45 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

Cho hai biểu thức :

$A = (\sqrt{20} - \sqrt{45} + 3 \sqrt{5}) : \sqrt{5}$

$B = \frac{x + 2 \sqrt{x}}{\sqrt{x}} + \frac{x - 9}{\sqrt{x} + 3}$

a, Rút gọn các biểu thức a, b

Xem đáp án

a, Rút gọn

$\begin{array}{l} A = (\sqrt{20} - \sqrt{45} + 3 \sqrt{5}) : \sqrt{5} = (2 \sqrt{5} - 3 \sqrt{5} + 3 \sqrt{5}) : \sqrt{5} \\ = 2 \sqrt{5} : \sqrt{5} = 2 \end{array}$

$\begin{array}{l} B = \frac{x + 2 \sqrt{x}}{\sqrt{x}} + \frac{x - 9}{\sqrt{x} + 3} (x > 0) \\ = \frac{\sqrt{x} . (\sqrt{x} + 2)}{\sqrt{x}} + \frac{(\sqrt{x} - 3) (\sqrt{x} + 3)}{\sqrt{x} + 3} \\ = \sqrt{x} + 2 + \sqrt{x} - 3 = 2 \sqrt{x} - 1 \end{array}$

Câu 2:

b, Tìm các giá trị của x sao cho giá trị biểu thức B bằng giá trị biểu thức A

Xem đáp án

b, Với x> 0 ta có B= A

$\Rightarrow 2 \sqrt{x} - 1 = 2 \Leftrightarrow \sqrt{x} = \frac{3}{2} \Leftrightarrow x = \frac{9}{4} (t m)$

Vậy $x = \frac{9}{4}$ với thì giá trị biểu thức B= A

Câu 3:

a) Tìm các giá trị của tham số m để đồ thị hai hàm số $y = (m + 4) x + 11$ và $y = x + m^{2} + 2$ cắt nhau tại một điểm trên trục tung.

Xem đáp án

a, Để đường thẳng $y = (m + 4) x + 11$ và $y = x + m^{2} + 2$ cắt nhau tại một điểm trên trục tung

$\Rightarrow \{\begin{cases} a \neq a' \\ b = b' \end{cases} \Leftrightarrow \{\begin{cases} m + 4 \neq 1 \\ 11 = m^{2} + 2 \end{cases} \Leftrightarrow \{\begin{cases} m \neq - 3 \\ m^{2} = 9 \end{cases} \Leftrightarrow \{\begin{cases} m \neq - 3 \\ [\begin{array}{l} m = 3 (t m) \\ m = - 3 (k t m) \end{array} \end{cases}$

Vậy m=3 với thì hai đường thẳng cắt nhau tại một điểm trên trục tung.

Câu 4:

b, Giải hệ phương trình: $\{\begin{cases} 3 x - \frac{2}{y + 1} = - \frac{1}{2} \\ 2 x + \frac{1}{y + 1} = 2 \end{cases}$

Xem đáp án

b, Xét hệ phương trình $\{\begin{cases} 3 x - \frac{2}{y + 1} = - \frac{1}{2} \\ 2 x + \frac{1}{y + 1} = 2 \end{cases}$ (ĐK $y \neq - 1)$

$\begin{array}{l} \Leftrightarrow \{\begin{cases} 3 x - \frac{2}{y + 1} = \frac{- 1}{2} \\ 4 x + \frac{2}{y + 1} = 4 \end{cases} \Leftrightarrow \{\begin{cases} 7 x = \frac{7}{2} \\ 2 x + \frac{1}{y + 1} = 2 \end{cases} \Leftrightarrow \{\begin{cases} x = \frac{1}{2} \\ \frac{1}{y + 1} = 1 \end{cases} \\ \Leftrightarrow \{\begin{cases} x = \frac{1}{2} \\ y + 1 = 1 \end{cases} \Leftrightarrow \{\begin{cases} x = \frac{1}{2} \\ y = 0 (t m) \end{cases} \end{array}$

Vậy hệ phương trình có nghiệm duy nhất $(x; y) = (\frac{1}{2}; 0)$

Câu 5:

1. Cho phương trình $x^{2} - 2 m x + 4 m - 4 = 0 (1)$ (x là ẩn số,m:tham số)

a, Giải phương trình khi m=1

Xem đáp án

1. Xét phương trình $x^{2} - 2 m x + 4 m - 4 = 0 (1)$

a,Với m=1 thay vào (1) $\Rightarrow x^{2} - 2 x = 0 \Leftrightarrow x (x - 2) = 0 \Leftrightarrow [\begin{array}{l} x = 0 \\ x = 2 \end{array}$

Vậy với m=1 thì phương trình có nghiệm x=0 hoặc x=2

Câu 6:

b, Xác định các giá trị của m để phương trình có hai nghiệm phân biệt $x_{1}, x_{2}$ thỏa mãn điều kiện $x_{1}^{2} + (x_{1} + x_{2}) x_{2} = 12$

Xem đáp án

b, Xét phương trình (1) ta có

$Δ = {(- 2 m)}^{2} - 4. (4 m - 4) = 4 m^{2} - 16 m + 16 = {(2 m - 4)}^{2} \geq 0 \forall m$

Để phương trình (1) có hai nghiệm phân biệt thì $Δ > 0 \Leftrightarrow 2 m - 4 \neq 0 \Leftrightarrow m \neq 2$

Áp dụng hệ thức Viet ta được: $\{\begin{cases} x_{1} + x_{2} = 2 m \\ x_{1} x_{2} = 4 m - 4 \end{cases}$

Theo đề bài ta có:

$\begin{array}{l} x_{1}^{2} + (x_{1} + x_{2}) x_{2} = 12 \\ \Leftrightarrow x_{1}^{2} + x_{2}^{2} + x_{1} x_{2} = 12 \\ \Leftrightarrow {(x_{1} + x_{2})}^{2} - x_{1} x_{2} = 12 \\ \Rightarrow {(2 m)}^{2} - (4 m - 4) = 12 \\ \Leftrightarrow 4 m^{2} - 4 m - 8 = 0 \\ \Leftrightarrow m^{2} - m - 2 = 0 \\ \Leftrightarrow (m + 1) (m - 2) = 0 \Leftrightarrow [\begin{array}{l} m = - 1 (t m) \\ m = 2 (k t m) \end{array} \end{array}$

Vậy với m=-1 thì phương trình có hai nghiệm $x_{1}; x_{2}$ phân biệt thỏa mãn $x_{1}^{2} + (x_{1} + x_{2}) x_{2} = 12$

Câu 7:

2. Bài toán có nội dung thực tế: Cho một thửa ruộng hình chữ nhật, biết rằng nếu chiều rộng tăng thêm 2m chiều dài giảm đi 2m thì diện tích thửa ruộng đó tăng thêm $30 m^{2};$ và nếu chiều rộng giảm đi 2m chiều dài tăng thêm 5m thì diện tích thửa ruộng giảm đi $20 m^{2};$ Tính diện tích thửa ruộng trên.

Xem đáp án

2. Gọi chiều dài của thửa ruộng là $x (m) (x > 2)$

Chiều rộng của thửa ruộng là $y (m) (y > 2)$

Diện tích của thửa ruộng là $x y (m^{2})$

Theo đề bài ta có hệ phương trình: $\{\begin{cases} (x - 2) (y + 2) = x y + 30 \\ (x + 5) (y - 2) = x y - 20 \end{cases}$

$\Leftrightarrow \{\begin{cases} 2 x - 2 y = 34 \\ - 2 x + 5 y = - 10 \end{cases} \Leftrightarrow \{\begin{cases} x = 25 (t m) \\ y = 8 (t m) \end{cases}$

Vậy thửa ruộng có chiều dài 25m, chiều rộng là 8m

Diện tích thửa ruộng là $25.8 = 200 (m^{2})$

Câu 8:

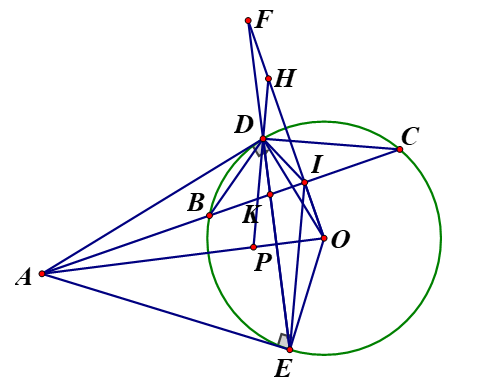
1.Từ điểm A nằm ngoài đường tròn (O) vẽ hai tiếp tuyến AD, AE (D,E là các tiếp điểm). Vẽ cát tuyến ABC của đường tròn (O) sao cho điểm B nằm giữa hai điểm A và tia C nằm giữa hai tia AD và AO Từ điểm O kẻ $O I ⊥ A C$ tại I

a, Chứng minh $A, D, I, O, E$ năm điểm cùng nằm trên một đường tròn.

Xem đáp án

1.Từ điểm A nằm ngoài đường tròn (O) vẽ hai tiếp tuyến AD, AE (D,E là các tiếp điểm). (ảnh 1)

1, a) Xét (O) ta có:

$\hat{A D O} = 90^{0}$ ( AD là tiếp tuyến của(O) )

$\hat{A I O} = 90^{0}$ $(O I ⊥ A C)$

$\hat{A E O} = 90^{0} (A E$ là tiếp tuyến của (O))

$\to$ 5 điểm $A, D, I, E, O$ cùng nằm trên đường tròn đường kính AO

Câu 9:

b, Chứng minh IA là tia phân giác của $\hat{D I E}$ và $A B . A C = A D^{2}$

Xem đáp án

b) Xét đường tròn đường kính AO

Ta có: $\hat{A I D} = \hat{A E D}$ (hai góc nội tiếp cùng chắn $\overset{⏜}{A D})$

$\hat{A I E} = \hat{A D E}$ (hai góc nội tiếp cùng chắn $\overset{⏜}{A E})$

Mà $\hat{A E D} = \hat{A D E} (Δ A D E$ cân tại A do AD = AE là hai tiếp tuyến cắt nhau)

$\Rightarrow \hat{A I D} = \hat{A I E} \Rightarrow I A$ là tia phân giác của $\hat{D I E}$

*)Xét $Δ A B D$ và $Δ A D C$ có:

$\hat{D A C}$ chung; $\hat{A D B} = \hat{A C D} ($ góc tạo bởi tiếp tuyến và dây cung và góc nội tiếp cùng chắn $\overset{⏜}{B D})$

$\Rightarrow Δ A B D ~ Δ A D C (g . g) \Rightarrow \frac{A B}{A D} = \frac{A D}{A C} \Rightarrow A B . A C = A D^{2} (d f c m)$

Câu 10:

c, Gọi K và F lần lượt là giao điểm của ED với ACvà EI Qua điểm D vẽ đường thẳng song song với IE cắt OF và IC lần lượt tại H và P Chứng minh là D trung điểm của HP

Xem đáp án

c, Ta có: $P D / / I E (g t) \Rightarrow \frac{D P}{I E} = \frac{D K}{K E}$ (hệ quả Ta let ) (1)

Vì IA là tia phân giác $\hat{D I E} (c m t) \Rightarrow I K$ là tia phân giác $Δ D I E$

$\Rightarrow \frac{D K}{K E} = \frac{I D}{I E}$ (tính chất tia phân giác ) (2)

Mà $I F ⊥ I A (O I ⊥ A C) \Rightarrow I F$ là đường phân giác ngoài $Δ D I E \Rightarrow \frac{F D}{F E} = \frac{I D}{I E} (3)$

Xét $Δ F E I$ có $D H / / I E (g t) \Rightarrow \frac{D H}{I E} = \frac{F D}{F E} (4)$ (hệ quả Ta let)

Từ $(2), (3), (4) \Rightarrow \frac{D H}{I E} = \frac{D K}{K E} (5)$

Từ (1) và (5) $\Rightarrow \frac{D P}{I E} = \frac{D H}{I E}$ hay $D P = D H$

Vậy D là trung điểm của $H P (d f c m)$

Câu 11:

2. Một hình trụ có diện tích xung quanh $140 π (c m^{2})$ và chiều cao h= 7(cm) Tính thể tích của hình trụ đó

Xem đáp án

Diện tích xung quanh hình trụ là $140 π (c m^{2})$

$\Rightarrow S_{x q} = 2 π R h = 140 π \Leftrightarrow 2 π R .7 = 140 π \Leftrightarrow R = 10 (c m)$

Thể tích hình trụ là $V = π R^{2} h = π {.10}^{2} .7 = 700 π (c m^{3})$

Câu 12:

a, Cho x,y,z là ba số dương. Chứng minh : $(x + y + z) (\frac{1}{x} + \frac{1}{y} + \frac{1}{z}) \geq 9$

Xem đáp án

a, Ta có: $(x + y + z) (\frac{1}{x} + \frac{1}{y} + \frac{1}{z})$

$\begin{array}{l} = 1 + \frac{x}{y} + \frac{x}{z} + \frac{y}{x} + 1 + \frac{y}{z} + \frac{z}{x} + \frac{z}{y} + 1 \\ = (\frac{x}{y} + \frac{y}{x}) + (\frac{x}{z} + \frac{z}{x}) + (\frac{y}{z} + \frac{z}{y}) + 3 \end{array}$

Áp dụng bđt Cô si cho các số $x, y, z > 0$

$\frac{x}{y} + \frac{y}{x} \geq 2 \sqrt{\frac{x}{y} . \frac{y}{x}} = 2$

$\frac{x}{z} + \frac{z}{x} \geq 2 \frac{y}{z} + \frac{z}{y} \geq 2$

Suy ra $(x + y + z) (\frac{1}{x} + \frac{1}{y} + \frac{1}{z}) \geq 2 + 2 + 2 + 3 = 9 (d f c m)$

Dấu "=" xảy ra $\Leftrightarrow x = y = z > 0$

Câu 13:

b, Cho a,b,c là ba số dương thỏa mãn a +b+c =6 Tìm giá trị lớn nhất của biểu thức: $A = \frac{a b}{a + 3 b + 2 c} + \frac{b c}{b + 3 c + 2 a} + \frac{c a}{c + 3 a + 2 b}$

Xem đáp án

b, Áp dụng câu a $\Rightarrow \frac{1}{x} + \frac{1}{y} + \frac{1}{z} \geq \frac{9}{x + y + z}$

Ta có: $\frac{a b}{a + 3 b + 2 c} = \frac{a b}{(a + c) + (b + c) + 2 b} \leq \frac{1}{9} (\frac{a b}{a + c} + \frac{a b}{b + c} + \frac{a}{2})$

Tương tự:

$\begin{array}{l} \frac{b c}{2 a + b + 3 c} = \frac{b c}{(a + b) + (a + c) + 2 c} \leq \frac{1}{9} (\frac{b c}{a + b} + \frac{b c}{a + c} + \frac{b}{2}) \\ \frac{a c}{3 a + 2 b + c} = \frac{a c}{(a + b) + (b + c) + 2 a} \leq \frac{1}{9} (\frac{a c}{a + b} + \frac{a c}{b + c} + \frac{c}{2}) \end{array}$

Suy ra

$A \leq \frac{1}{9} . (\frac{a c + b c}{a + b} + \frac{a b + a c}{b + c} + \frac{a b + b c}{a + c}) = \frac{a + b + c}{6} = \frac{6}{6} = 1 \Rightarrow A \leq 1$

Vậy $M a x A = 1 \Leftrightarrow a = b = c = 2$

Bắt đầu thi ngay

CHỌN BỘ SÁCH BẠN MUỐN XEM

Tổng hợp đề thi chính thức vào 10 môn Toán năm 2019 có đáp án (Phần 1)

Tổng hợp đề thi chính thức vào 10 môn Toán năm 2019 có đáp án (Phần 1)- Đề 27

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm