12 câu hỏi trắc nghiệm thuộc Tổng hợp đề thi chính thức vào 10 môn Toán năm 2019 có đáp án (Phần 1)- Đề 15

Câu 1:

a, Tính $A = \sqrt{12} + \sqrt{18} - \sqrt{8} - 2 \sqrt{3}$

a, $A = \sqrt{12} + \sqrt{18} - \sqrt{8} - 2 \sqrt{3}$

$\begin{array}{l} = \sqrt{3.4} + \sqrt{9.2} - \sqrt{4.2} - 2 \sqrt{3} \\ = 2 \sqrt{3} + 3 \sqrt{2} - 2 \sqrt{2} - 2 \sqrt{3} \\ = \sqrt{2} \end{array}$

Câu 2:

Cho biểu thức $B = \sqrt{9 x + 9} + \sqrt{4 x + 4} + \sqrt{x + 1}$ với $x \geq - 1.$ Tìm x sao cho B có giá trị là 18

Xem đáp án

b, $B = \sqrt{9 x + 9} + \sqrt{4 x + 4} + \sqrt{x + 1}$

$\begin{array}{l} = \sqrt{9 (x + 1)} + \sqrt{4 (x + 1)} + \sqrt{x + 1} \\ = 3 \sqrt{x + 1} + 2 \sqrt{x + 1} + \sqrt{x + 1} = 6 \sqrt{x + 1} \end{array}$

Ta có: $B = 18 \Leftrightarrow 6 \sqrt{x + 1} = 18 \Leftrightarrow \sqrt{x + 1} = 3 \Rightarrow x + 1 = 9 \Leftrightarrow x = 8 (t m)$

Vậy x= 3 thì B=18

Câu 3:

Giải hệ phương trình $\{\begin{cases} x + 2 y = 3 \\ 4 x + 5 y = 6 \end{cases}$

Xem đáp án

$a) \{\begin{cases} x + 2 y = 3 \\ 4 x + 5 y = 6 \end{cases} \Leftrightarrow \{\begin{cases} 4 x + 8 y = 12 \\ 4 x + 5 y = 6 \end{cases} \Leftrightarrow \{\begin{cases} 3 y = 6 \\ x = 3 - 2 y \end{cases} \Leftrightarrow \{\begin{cases} x = - 1 \\ y = 2 \end{cases}$

Vậy hệ phương trình có nghiệm $(x; y) = (- 1; 2)$

Câu 4:

Giải phương trình $4 x^{4} + 7 x^{2} - 2 = 0$

Xem đáp án

b) Đặt $t = x^{2} (t \geq 0)$ . Khi đó phương trình trở thành

$\begin{array}{l} 4 t^{2} + 7 t - 2 = 0 \Leftrightarrow 4 t^{2} + 8 t - t - 2 = 0 \\ \Leftrightarrow 4 t (t + 2) - (t + 2) = 0 \Leftrightarrow (t + 2) (4 t - 1) = 0 \\ \Leftrightarrow [\begin{array}{l} t = - 2 (k t m) \\ t = \frac{1}{4} (t m) \Rightarrow x = \pm \frac{1}{2} \end{array} \end{array}$

Vậy phương trình đã cho có tập nghiệm $S = \{- \frac{1}{2}; \frac{1}{2}\}$

Câu 5:

b, Tìm tọa độ hai giao điểm A và B của hai đồ thị đó. Tính khoảng cách từ điểm $M (- 2; 0)$ đến đường thẳng AB

Xem đáp án

Xét phương trình hoành độ giao điểm của đường thẳng $d : y = - 2 x + 4$ và parabol (P): $y = 2 x^{2}$

$\begin{array}{l} \Leftrightarrow x^{2} + x - 2 = 0 \Leftrightarrow x^{2} - x + 2 x - 2 = 0 \\ \Leftrightarrow (x - 1) (x + 2) = 0 \Leftrightarrow [\begin{array}{l} x - 1 = 0 \\ x + 2 = 0 \end{array} \Leftrightarrow [\begin{array}{l} x = 1 \Rightarrow y = 2 \\ x = - 2 \Rightarrow y = 8 \end{array} \end{array}$

Vậy giao điểm của (P) và (d) là

Kẻ $M H ⊥ A B (M \in A B) .$ Nhận xét thấy khoảng cách từ $M (- 2; 0)$ xuống đường thẳng AB chính là MH

Lại thấy $B (- 2; 8), M (- 2; 0) \Rightarrow$ Phương trình đường thẳng BM là $x = - 2 \Rightarrow B M ⊥ O x$ hay $B M ⊥ M C$ suy ra $Δ B M C$ vuông tại M.

Ta lại có: $B (- 2; 8); M (- 2; 0); C (2,0) \Rightarrow B M = 8, C M = 4$

Xét $Δ B M C$ vuông tại M có MH là đường cao nên :

$\frac{1}{M H^{2}} = \frac{1}{B M^{2}} + \frac{1}{M C^{2}} = \frac{1}{8^{2}} + \frac{1}{4^{2}} = \frac{5}{64} \Leftrightarrow M H = \frac{8 \sqrt{5}}{5}$

Vậy khoảng cách cần tìm là $M H = \frac{8 \sqrt{5}}{5}$

Câu 6:

Cho hai hàm số $y = 2 x^{2}$ và $y = - 2 x + 4$

a, Vẽ đồ thị các hàm số trên cùng một mặt phẳng tọa độ

Xem đáp án

a, Học sinh tự vẽ đồ thị

Câu 7:

Cho phương trình $4 x^{2} + (m^{2} + 2 m - 15) x + {(m + 1)}^{2} - 20 = 0$ với m là tham số. Tìm tất cả các giá trị của m để phương trình đã cho có hai nghiệm $x_{1}, x_{2}$ thỏa mãn hệ thức $x_{1}^{2} + x_{2} + 2019 = 0$

Xem đáp án

Phương trình đã cho có hai nghiệm $x_{1}, x_{2} \Leftrightarrow Δ \geq 0$

$\begin{array}{l} \Leftrightarrow {(m^{2} + 2 m - 15)}^{2} - 16 [{(m + 1)}^{2} - 20] \geq 0 \\ \Leftrightarrow {[{(m + 1)}^{2} - 16]}^{2} - 16 {(m + 1)}^{2} + 320 \geq 0 \\ \Leftrightarrow {(m + 1)}^{4} - 32. {(m + 1)}^{2} + 256 - 16 {(m + 1)}^{2} + 320 \geq 0 \\ \Leftrightarrow {(m + 1)}^{4} - 48. {(m + 1)}^{2} + 576 \geq 0 \\ \Leftrightarrow {(m + 1)}^{4} - 2.24. {(m + 1)}^{2} + 24^{2} \geq 0 \\ [{(m + 1)}^{2} - 24] \geq 0 \forall m \end{array}$

Nên phương trình đã cho luôn có hai nghiệm phân biệt với mọi m

Áp dụng hệ thức Vi-et ta có: $\begin{array}{l} \{\begin{cases} x_{1} + x_{2} = - \frac{m^{2} + 2 m - 15}{4} = - \frac{{(m + 1)}^{2} - 16}{4} = - \frac{{(m + 1)}^{2}}{4} + 4 \\ x_{1} x_{2} = \frac{{(m + 1)}^{2} - 20}{4} = \frac{{(m + 1)}^{2}}{4} - 5 \end{cases} \\ \Rightarrow x_{1} + x_{2} + x_{1} x_{2} = - 1 (*) \end{array}$

Theo đề bài ta có: $x_{1}^{2} + x_{2} + 2019 = 0 \Leftrightarrow x_{2} = - x_{1}^{2} - 2019$

Thay vào (*) ta có:

$\begin{array}{l} \Leftrightarrow x_{1}^{3} + x_{1}^{2} + 2018 x_{1} + 2018 = 0 \Leftrightarrow x_{1}^{2} (x_{1} + 1) + 2018 (x_{1} + 1) = 0 \\ \Leftrightarrow (x_{1} + 1) (x_{1}^{2} + 2018) = 0 \Leftrightarrow x_{1} + 1 = 0 (x_{1}^{2} + 2018 > 0) \\ \Leftrightarrow x_{1} = - 1 \Rightarrow x_{2} = - 1 - 2019 = - 2020 \end{array}$

Mặt khác $x_{1} x_{2} = \frac{{(m + 1)}^{2}}{4} - 5$

$\begin{array}{l} \Leftrightarrow 2020 = \frac{{(m + 1)}^{2}}{4} - 5 \Leftrightarrow 2025.4 = {(m + 1)}^{2} \\ \Leftrightarrow {(m + 1)}^{2} = 8100 \Leftrightarrow [\begin{array}{l} m + 1 = 90 \\ m + 1 = - 90 \end{array} \Leftrightarrow [\begin{array}{l} m = 89 \\ m = - 91 \end{array} \end{array}$

Vậy $m \in \{89; - 91\}$ thỏa mãn điều kiện bài toán

Câu 8:

Một mảnh đất hình chữ nhật có diện tích $80 m^{2} .$ Nếu giảm chiều rộng 3m và tăng chiều dài 10m thì diện tích mảnh đất tăng thêm $20 m^{2} .$ Tìm kích thước của mảnh đất

Xem đáp án

Gọi chiều rộng của mảnh đất là x (mét) $(x > 3)$

Chiều dài của mảnh đất là y mét ( $y > x > 3)$

Diện tích mảnh đất là $80 m^{2}$ nên ta có phương trình $x y = 80 (1)$

Nếu giảm chiều rộng đi 3m thì chiều rộng mới là $x - 3 (m)$

Nếu tăng chiều dài lên 10m thì chiều dài mới là $y + 10 (m)$

Diện tích mảnh đất mới là $80 + 20 = 100 (m^{2})$ nên ta có phương trình:

$(x - 3) (y + 10) = 100 (2)$

Từ (1) và (2) ta có hệ phương trình:

$\begin{array}{l} \{\begin{cases} x y = 80 \\ (x - 3) (y + 10) = 100 \end{cases} \Leftrightarrow \{\begin{cases} x y = 80 \\ x y - 3 y + 10 x - 30 - 100 = 0 \end{cases} \\ \Leftrightarrow \{\begin{cases} x y = 80 \\ 80 + 10 x - 3 y - 130 = 0 \end{cases} \Leftrightarrow \{\begin{cases} 10 x y = 800 \\ 10 x + 3 y + 50 \end{cases} \Leftrightarrow \{\begin{cases} (3 y + 50) y = 800 \\ 10 x = 3 y + 50 \end{cases} \\ \Leftrightarrow \{\begin{cases} 3 y^{2} + 50 y - 800 = 0 \\ 10 x = 3 y + 50 \end{cases} \Leftrightarrow \{\begin{cases} [\begin{array}{l} y = 10 (t m) \\ y = - \frac{80}{3} (k t m) \end{array} \\ x = \frac{80}{y} \end{cases} \Leftrightarrow \{\begin{cases} x = 8 \\ y = 10 \end{cases} (t m) \end{array}$

Vậy chiều dài mảnh đất là 10m và chiều rộng mảnh đất là 8m

Câu 9:

Một mảnh đất hình chữ nhật có diện tích $80 m^{2} .$ Nếu giảm chiều rộng 3m và tăng chiều dài 10m thì diện tích mảnh đất tăng thêm $20 m^{2} .$ Tìm kích thước của mảnh đất

Xem đáp án

Gọi chiều rộng của mảnh đất là x (mét) $(x > 3)$

Chiều dài của mảnh đất là y mét ( $y > x > 3)$

Diện tích mảnh đất là $80 m^{2}$ nên ta có phương trình $x y = 80 (1)$

Nếu giảm chiều rộng đi 3m thì chiều rộng mới là $x - 3 (m)$

Nếu tăng chiều dài lên 10m thì chiều dài mới là $y + 10 (m)$

Diện tích mảnh đất mới là $80 + 20 = 100 (m^{2})$ nên ta có phương trình:

$(x - 3) (y + 10) = 100 (2)$

Từ (1) và (2) ta có hệ phương trình:

$\begin{array}{l} \{\begin{cases} x y = 80 \\ (x - 3) (y + 10) = 100 \end{cases} \Leftrightarrow \{\begin{cases} x y = 80 \\ x y - 3 y + 10 x - 30 - 100 = 0 \end{cases} \\ \Leftrightarrow \{\begin{cases} x y = 80 \\ 80 + 10 x - 3 y - 130 = 0 \end{cases} \Leftrightarrow \{\begin{cases} 10 x y = 800 \\ 10 x + 3 y + 50 \end{cases} \Leftrightarrow \{\begin{cases} (3 y + 50) y = 800 \\ 10 x = 3 y + 50 \end{cases} \\ \Leftrightarrow \{\begin{cases} 3 y^{2} + 50 y - 800 = 0 \\ 10 x = 3 y + 50 \end{cases} \Leftrightarrow \{\begin{cases} [\begin{array}{l} y = 10 (t m) \\ y = - \frac{80}{3} (k t m) \end{array} \\ x = \frac{80}{y} \end{cases} \Leftrightarrow \{\begin{cases} x = 8 \\ y = 10 \end{cases} (t m) \end{array}$

Vậy chiều dài mảnh đất là 10m và chiều rộng mảnh đất là 8m

Câu 10:

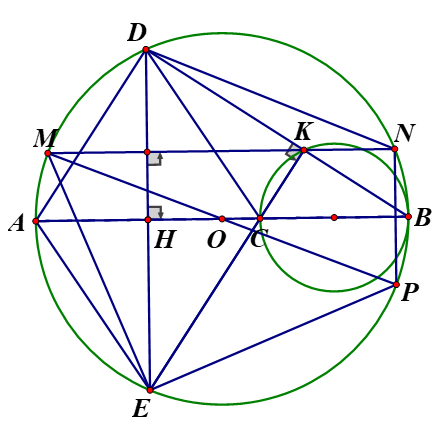
Cho đường tròn (O) tâm O, đường kính AB và C là điểm nằm trên đoạn thẳng OB ( với $C \neq B)$ . Kẻ dây DE của đường tròn (O) vuông góc với AC tại trung điểm H của AC Gọi K là giao điểm thứ hai của BD với đường tròn đường kính BC

Chứng minh tứ giác $D H C K$ là tứ giác nội tiếp

Xem đáp án

a)

Cho đường tròn (O) tâm O, đường kính AB và C là điểm nằm trên đoạn thẳng OB (ảnh 1)

Ta có : $\hat{D H B} = 90^{0}$ ( $D E ⊥ A B$ tại H) $\Rightarrow \hat{D H C} = 90^{0}$

$\hat{C K B} = 90^{0}$ (góc nội tiếp chắn nửa đường tròn đường kính BC) $\Rightarrow \hat{C K D} = 90^{0}$

Xét tứ giác DHCK có $\hat{D H C} + \hat{C K D} = 180^{0},$ mà hai góc ở vị trí đối diện nên tứ giác DHCK nội tiếp (tứ giác có tổng hai góc đối bằng $180^{0})$ (đpcm)

Câu 11:

b, Chứng minh CE song song với AD và ba điểm E, C , K thẳng hàng

Xem đáp án

a) Có $D E ⊥ A B \Rightarrow H D = H E$ (đường kính dây cung)

Lại có: $H A = H C (g t)$ nên tứ giác $D A E C$ là hình bình hành $\Rightarrow C E / / D A (d f c m)$

Lại có $\hat{C K B} = 90^{0}$ (góc nội tiếp chắn nửa đường tròn đường kính BC) $\Rightarrow C K ⊥ K B (1)$

Mà $\hat{A D B} = 90^{0}$ (góc nội tiếp chắn nửa đường tròn đường kính AB) $\Rightarrow A D ⊥ D B (2)$

Từ (1) và (2) suy ra $C K / / A D$ (từ vuông góc đến song song)

Mà $C E / / A D (c m t)$ nên theo tiên đề Oclit suy ra ba điểm $E, C, K$ thẳng hàng.

Câu 12:

c, Đường thẳng qua K vuông góc với DE cắt đường tròn (O) tại hai điểm M và N (với M thuộc cung nhỏ $\overset{⏜}{A D})$ . Chứng minh $E M^{2} + D N^{2} = A B^{2}$

Xem đáp án

Kẻ đường kính MP của đường tròn (O) . Nối N với P cắt AB tai I . Nối E với P, E với B.

Có $\hat{M N P} = 90^{0}$ (góc nội tiếp chắn nửa đường tròn) $\Rightarrow M N ⊥ N P$

Mà $M N ⊥ D E (g t)$ nên $N P / / D E \Rightarrow D N P E$ là hình thang

Lại có $D E ⊥ A B, N P / / D E \Rightarrow N P ⊥ A B \Rightarrow I$ là trung điểm của NP (tính chất đường kính dây cung) $\Rightarrow B$ là điểm chính giữa cung NP

$\Rightarrow s d \overset{⏜}{N B} = s d \overset{⏜}{P B}$

Dễ thấy tam giác BDE cân tại B (đường cao BH cũng là đường trung tuyến)

$\Rightarrow B D = B E \Rightarrow s d \overset{⏜}{B D} = s d \overset{⏜}{B E}$

$\Rightarrow s d D B - s d B N = s d E B - s d B P \Rightarrow s d D N = s d E P \Rightarrow D N = E P$ (hai dây bằng nhau căng hai cung bằng nhau)

Do đó: $E M^{2} + D N^{2} = E M^{2} + E P^{2} = M P^{2}$ (Do tam giác MEP vuông tại E), mà $M P = A B$ (=đường kính)

Vậy $E M^{2} + E P^{2} = A B^{2} (d f c m)$

CHỌN BỘ SÁCH BẠN MUỐN XEM

Tổng hợp đề thi chính thức vào 10 môn Toán năm 2019 có đáp án (Phần 1)

Tổng hợp đề thi chính thức vào 10 môn Toán năm 2019 có đáp án (Phần 1)- Đề 15

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm