12 câu hỏi trắc nghiệm thuộc Tổng hợp đề thi chính thức vào 10 môn Toán năm 2019 có đáp án (Phần 1)- Đề 7

Tổng hợp đề thi chính thức vào 10 môn Toán năm 2019 có đáp án (Phần 1)

Đề số 1
Đề số 2
Đề số 3
Đề số 4
Đề số 5
Đề số 6
Đề số 7
Đề số 8
Đề số 9
Đề số 10
Đề số 11
Đề số 12
Đề số 13
Đề số 14
Đề số 15
Đề số 16
Đề số 17
Đề số 18
Đề số 19
Đề số 20
Đề số 21
Đề số 22
Đề số 23
Đề số 24
Đề số 25
Đề số 26
Đề số 27
Đề số 28
Đề số 29
Đề số 30

Tổng hợp đề thi chính thức vào 10 môn Toán năm 2019 có đáp án (Phần 1)- Đề 7

6644 lượt thi
12 câu hỏi
45 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

Rút gọn biểu thức $A = \sqrt{27} - \sqrt{12}$

Xem đáp án

a) Ta có: $A = \sqrt{27} - \sqrt{12} = 3 \sqrt{3} - 2 \sqrt{3} = \sqrt{3}$

Câu 2:

Giải hệ phương trình: $\{\begin{cases} 7 x - 3 y = 5 \\ x + 3 y = 3 \end{cases}$

Xem đáp án

b, $\{\begin{cases} 7 x - 3 y = 5 \\ x + 3 y = 3 \end{cases} \Leftrightarrow \{\begin{cases} 8 x = 8 \\ y = \frac{3 - x}{3} \end{cases} \Leftrightarrow \{\begin{cases} x = 1 \\ y = \frac{2}{3} \end{cases}$

Vậy hệ phương trình có nghiệm $(x; y) = (1; \frac{2}{3})$

Câu 3:

a,Trong mặt phẳng tọa độ (Oxy )cho parabol $(P) : y = - 2 x^{2}$ . Vẽ (P)

Xem đáp án

a, Học sinh tự vẽ Parabol

Câu 4:

b, Tìm m để đường thẳng $y = (5 m - 2) x + 2019$ song song với đường thẳng $y = x + 3$

Xem đáp án

Đường thẳng $y = (5 m - 2) x + 2019$ song song với đường thẳng $y = x + 3$

$\Leftrightarrow \{\begin{cases} 5 m - 2 = 1 \\ 2019 \neq 3 (l u o n .... d u n g) \end{cases} \Leftrightarrow 5 m = 3 \Leftrightarrow m = \frac{3}{5}$

Vậy $m = \frac{3}{5}$ thỏa mãn bài toán.

Câu 5:

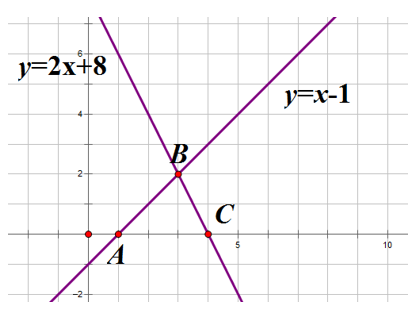
c, Hai đường thẳng $y = x - 1$ và $y = - 2 x + 8$ cắt nhau tại điểm B và lần lượt cắt trục Ox tại điểm A,C (hình vẽ). Xác định tọa độ các điểm A, B, C và tính diện tích tam giác ABC

Xem đáp án

Ta có:

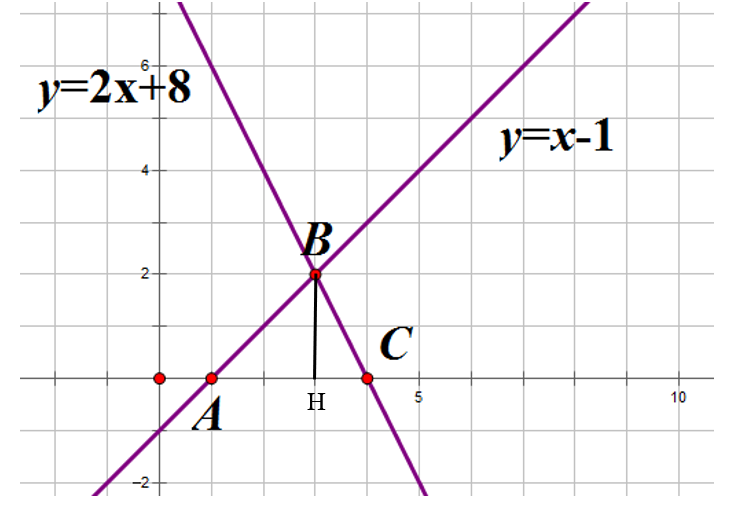
c) Hai đường thẳng y=x-1 và y= -2x+8 cắt nhau tại điểm B và lần lượt cắt trục Ox tại điểm A,C (hình vẽ). (ảnh 1)

A (1; 0) B (3; 2) C (4; 0)

Gọi H là hình chiếu vuông góc của B trên AC, ta có $S_{A B C} = \frac{1}{2} B H . A C$

Ta có : $\{\begin{cases} B H = y_{B} = 2 \\ A C = x_{C} - x_{A} = 4 - 1 = 3 \end{cases} \Rightarrow S_{A B C} = \frac{1}{2} B H . A C = \frac{1}{2} .2.3 = 3 (d v d t)$

Câu 6:

a, Giải phương trình: $x^{2} + 2 x - 3 = 0$

Xem đáp án

a, Phương trình $x^{2} + 2 x - 3 = 0$ có dạng $a + b + c = 1 + 2 - 3 = 0$

Nên phương trình có hai nghiệm phân biệt $\{\begin{cases} x_{1} = 1 \\ x_{2} = \frac{c}{a} = - 3 \end{cases}$

Vậy phương trình đã cho có tập nghiệm $S = \{1; - 3\}$

Câu 7:

b, Tìm m để phương trình $x^{2} - 2 (m + 1) x + m^{2} + 3 m - 7 = 0$ vô nghiệm

Xem đáp án

b, Phương trình đã cho vô nghiệm $\Leftrightarrow Δ' < 0$

$\begin{array}{l} \Leftrightarrow {(m + 1)}^{2} - m^{2} - 3 m + 7 < 0 \\ \Leftrightarrow m^{2} + 2 m + 1 - m^{2} - 3 m + 7 < 0 \\ \Leftrightarrow - m + 8 < 0 \Leftrightarrow m > 8 \end{array}$

Vậy với m >8 thì phương trình đã cho vô nghiệm.

Câu 8:

Cho tam giác ABC vuông tại A, đường cao AH Biết $A B = 3 c m, A C = 4 c m .$ Tính độ dài đường cao AH tính $\cos \hat{A C B}$ và chu vi tam giác

Xem đáp án

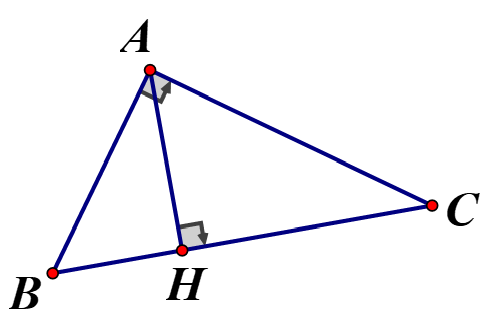
Cho tam giác ABC vuông tại A, đường cao AH Biết AB= 3cm , AC= 4cm Tính độ dài đường cao AH (ảnh 1)

Áp dụng định lý Pytago trong $Δ A B C$ vuông tại C ta có: $B C^{2} = A C^{2} + A B^{2} = 3^{2} + 4^{2} = 5^{2} \Rightarrow B C = 5 c m$

Áp dụng hệ thức lượng trong $Δ A B C$ vuông tại A có đường cao AH ta có:

$A H . B C = A B . A C \Leftrightarrow A H = \frac{A B . A C}{B C} = \frac{3.4}{5} = 2,4 c m$

Ta có: $\cos \hat{A C B} = \frac{A C}{B C} = \frac{4}{5}$

Câu 9:

Sau kỳ thi tuyển sinh vào lớp 10 năm học 2019-2020, học sinh hai lớp 9A và 9B tặng lại thư viện trường 738 quyển sách gồm hai loại sách giáo khoa và sách tham khảo. Trong đó, mỗi học sinh lớp 9A tặng 6 quyển sách giáo khoa và 3 quyển sách thâm khảo, mỗi học sinh lớp tặng 5 quyển sách giáo khoa và 4 quyển sách tham khảo. Biết số sách giáo khoa nhiều hơn số sách tham khảo là 166 quyển. Tính số học sinh của mỗi lớp.

Xem đáp án

Gọi số học sinh lớp 9A là x (học sinh) $(x \in ℕ *)$

Gọi số học sinh lớp 9B là y (học sinh) $(y \in ℕ *)$

Số sách giáo khoa lớp 9A tặng cho trường là: 6x (quyển sách)

Số sách tham khảo lớp 9A tặng cho trường là: 3x (quyển sách)

Số sách giáo khoa lớp tặng cho trường là:5y (quyển sách)

Số sách tham khảo lớp 9B tặng cho trường là : 4y (quyển sách)

Tổng số sách cả hai lớp tặng cho trường là quyển nên ta có phương trình:

$6 x + 3 x + 5 y + 4 y = 738 \Leftrightarrow 9 x + 9 y = 738 \Leftrightarrow x + y = 82 (1)$

Tổng số sách giáo khoa nhiều hơn số sách tham khảo là 166 quyển nên ta có phương trình:

$6 x + 5 y - (3 x + 4 y) = 166 \Leftrightarrow 3 x + y = 166 (2)$

Từ (1) và (2) ta có hệ phương trình: $\{\begin{cases} x + y = 82 \\ 3 x + y = 166 \end{cases} \Leftrightarrow \{\begin{cases} 2 x = 84 \\ y = 82 - x \end{cases} \Leftrightarrow \{\begin{cases} x = 42 (t m) \\ y = 40 (t m) \end{cases}$

Vậy lớp 9A có 42 học sinh, lớp 9B có 40 học sinh.

Câu 10:

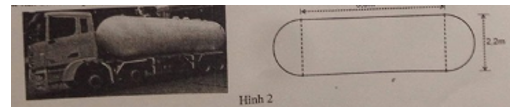
Một bồn chứa xăng đặt trên xe gồm hai nửa hình cầu có đường kính 2,2m và một hình trụ có chiều dài 3,5m (hình vẽ). Tính thể tích của bồn chứa xăng (kết quả làm tròn đến chữ số thập phân thứ hai sau dấu phẩy).

b) Một bồn chứa xăng đặt trên xe gồm hai nửa hình cầu có đường kính 2,2m và một hình trụ có chiều dài 3,5m (hình vẽ). (ảnh 1)

Xem đáp án

Bồn chứa xưng bao gồm 1 hình cầu và 1 hình trụ .

Ta có bán kính của hình cầu của bồn chứa xăng là : $R = 2,2 : 2 = 1,1 m$

$\Rightarrow$ Thể tích phần hình cầu của bồn chứa xăng là: $V_{1} = \frac{4}{3} π R^{3} = \frac{4}{3} {.3,14.1,1}^{3} \approx 5,57 (m^{3})$

Phần hình trụ của bồn chứa xăng có bán kính đáy là $R = 1,1 m$ và chiều cao là $h = 3,5 m$

$\Rightarrow$ Thể tích phần hình trụ của bồn chứa xăng là $V_{2} = π R^{2} h = {3,14.1,1}^{2} .3,5 = 13,3 (m^{3})$

Vậy thể tích của bồn chứa xăng là : $V = V_{1} + V_{2} = 5,57 + 13,3 = 18,87 (m^{3})$

Câu 11:

Cho tam giác ABC vuông cân ở A, đường cao $A H (H \in B C) .$ Trên AC lấy điểm M $(M \neq A, M \neq C)$ và vẽ đường tròn đường kính MC Kẻ BM cắt AH tại E và cắt đường tròn tại D. Đường thẳng AD cắt đường tròn tại S. Chứng minh rằng:

a) Tứ giác CDEF là một tứ giác nội tiếp

Xem đáp án

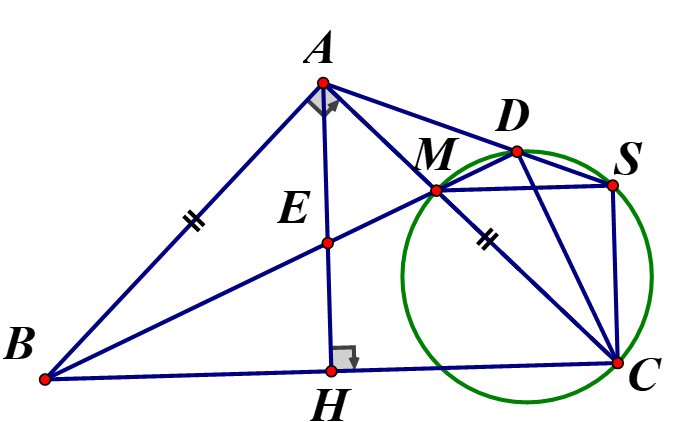
Cho tam giác ABC vuông cân ở A, đường cao AH (H thuộc BC) (ảnh 1)

Ta có $\hat{E H C} = 90^{0}$ (AH là đường cao của $Δ A B C)$

Ta có: $\hat{C D M} = 90^{0}$ (góc nội tiếp chắn nửa đường tròn đường kính MC)

$\Rightarrow \hat{C D E} = 90^{0}$

Xét tứ giác CDEH có $\hat{C D E} + \hat{C H E} = 90^{0} + 90^{0} = 180^{0}$ , suy ra tứ giác CDEH là tứ giác nội tiếp (tứ giác có tổng hai góc đối bằng

Câu 12:

b, $\hat{B C A} = \hat{A C S}$

Xem đáp án

b, Ta có: $\hat{C D E} = 90^{0} (c m t) \Rightarrow \hat{C D B} = 90^{0}$

Xét tứ giác ADCB có: $\hat{C D B} = \hat{C A B} = 90^{0} \Rightarrow$ Tứ giác ADCB là tứ giác nội tiếp (tứ giác có 2 đỉnh kề nhau cùng nhìn một cạnh dưới các góc bằng nhau).

$\Rightarrow \hat{B D A} = \hat{B C A}$ (hai góc nội tiếp cùng chắn cung AB).

Tứ giác CSDM nội tiếp đường tròn đường kính $C M \Rightarrow \hat{M C S} = \hat{A D M} = \hat{B D A}$ (góc ngoài và góc trong tại đỉnh đối diện của tứ giác nội tiếp)

$\Rightarrow \hat{B C A} = \hat{M C S} = \hat{A C S} (d f c m)$

Bắt đầu thi ngay

CHỌN BỘ SÁCH BẠN MUỐN XEM

Tổng hợp đề thi chính thức vào 10 môn Toán năm 2019 có đáp án (Phần 1)

Tổng hợp đề thi chính thức vào 10 môn Toán năm 2019 có đáp án (Phần 1)- Đề 7

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm