10 câu hỏi trắc nghiệm thuộc Tổng hợp đề thi chính thức vào 10 môn Toán năm 2019 có đáp án (Phần 1)- Đề 5

Tổng hợp đề thi chính thức vào 10 môn Toán năm 2019 có đáp án (Phần 1)

Đề số 1
Đề số 2
Đề số 3
Đề số 4
Đề số 5
Đề số 6
Đề số 7
Đề số 8
Đề số 9
Đề số 10
Đề số 11
Đề số 12
Đề số 13
Đề số 14
Đề số 15
Đề số 16
Đề số 17
Đề số 18
Đề số 19
Đề số 20
Đề số 21
Đề số 22
Đề số 23
Đề số 24
Đề số 25
Đề số 26
Đề số 27
Đề số 28
Đề số 29
Đề số 30

Tổng hợp đề thi chính thức vào 10 môn Toán năm 2019 có đáp án (Phần 1)- Đề 5

6693 lượt thi
10 câu hỏi
45 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

Rút gọn biểu thức

$a) A = \sqrt{45} - 2 \sqrt{20}$

Xem đáp án

$a) \sqrt{45} - 2 \sqrt{20} = \sqrt{9.5} - 2 \sqrt{4.5} = 3 \sqrt{5} - 2.2 \sqrt{5} = - \sqrt{5}$

Câu 2:

Rút gọn biểu thức $b) B = \frac{3 \sqrt{5} - \sqrt{27}}{\sqrt{3} - \sqrt{5}} - \sqrt{{(3 - \sqrt{12})}^{2}}$

Xem đáp án

$\begin{array}{l} b) B = \frac{3 \sqrt{5} - \sqrt{27}}{\sqrt{3} - \sqrt{5}} - \sqrt{{(3 - \sqrt{12})}^{2}} \\ = \frac{3 \sqrt{5} - 3 \sqrt{3}}{\sqrt{3} - \sqrt{5}} - |3 - \sqrt{12}| \\ = \frac{3 (\sqrt{5} - \sqrt{3})}{\sqrt{3} - \sqrt{5}} - (- 3 + \sqrt{12}) (d o 3^{2} < 12 \Rightarrow 3 < \sqrt{12}) \\ = - 3 + 3 - \sqrt{12} \\ = - \sqrt{12} = - 2 \sqrt{3} \end{array}$

Câu 3:

Giải hệ phương trình: $\{\begin{cases} 2 x - y = 4 \\ x + 4 = 5 \end{cases}$

Xem đáp án

$a) \{\begin{cases} 2 x - y = 4 \\ x + y = 5 \end{cases} \Leftrightarrow \{\begin{cases} 3 x = 9 \\ y = 5 - x \end{cases} \Leftrightarrow \{\begin{cases} x = 3 \\ y = 2 \end{cases}$

Vậy hệ phương trình có nghiệm là $(x; y) = (3; 2)$

Câu 4:

b, Cho hàm số $y = 3 x^{2}$ có đồ thị và đường thẳng $(d) : y = 2 x + 1.$ Tìm tọa độ giao điểm (P) của và (d) bằng phép tính.

Xem đáp án

Ta có phương trình hoành độ giao điểm :

$3 x^{2} = 2 x + 1 \Leftrightarrow 3 x^{2} - 2 x - 1 = 0 (*)$

Phương trình (*) có dạng $a + b + c = 3 - 2 - 1 = 0$ nên có hai nghiệm

$[\begin{array}{l} x = 1 \Rightarrow y = 3 \Rightarrow A (1; 3) \\ x = - \frac{1}{3} \Rightarrow y = \frac{1}{3} \Rightarrow B (\frac{- 1}{3}; \frac{1}{3}) \end{array}$

Vậy tọa độ giao điểm của (P) và (d) là $A (1; 3)$ và $(- \frac{1}{3}; \frac{1}{3})$

Câu 5:

Cho phương trình $x^{2} - 2 m x - 4 m - 5 = 0 (1)$ (m là tham số)

a, Giải phương trình khi m=2

Xem đáp án

Thay $m = - 2$ vào phương trình (1) ta có: $x^{2} + 4 x + 3 = 0$

$\begin{array}{l} \Leftrightarrow x^{2} + 3 x + x + 3 = 0 \Leftrightarrow x (x + 3) + (x + 3) = 0 \\ \Leftrightarrow (x + 3) (x + 1) = 0 \Leftrightarrow [\begin{array}{l} x + 3 = 0 \\ x + 1 = 0 \end{array} \Leftrightarrow [\begin{array}{l} x = - 3 \\ x = - 1 \end{array} \end{array}$

Vậy khi m = -2 thì phương trình có tập nghiệm $S = \{- 3; - 1\}$

Câu 6:

b,Chứng minh phương trình (1) luôn có hai nghiệm với mọi giá trị của m

Xem đáp án

Ta có: $Δ' = m^{2} - (- 4 m - 5) = m^{2} + 4 m + 5 = {(m + 2)}^{2} + 1 > 0 \forall m$

Do đó phương trình (1) luôn có hai nghiệm với mọi giá trị của m

Câu 7:

c, Gọi $x_{1}, x_{2}$ là hai nghiệm của phương trình (1). Tìm m để $\frac{1}{2} x_{1}^{2} - (m - 1) x_{1} + x_{2} - 2 m + \frac{33}{2} = 762019$

Xem đáp án

c) Áp dụng định lý Vi-et ta có: $\{\begin{cases} x_{1} + x_{2} = 2 m \\ x_{1} x_{2} = - 4 m - 5 \end{cases}$

Theo bài ra ta có:

$\begin{array}{l} \frac{1}{2} x_{1}^{2} - (m - 1) x_{1} + x_{2} - 2 m + \frac{33}{2} = 762019 \\ \Leftrightarrow x_{1}^{2} - 2 (m - 1) x_{1} + 2 x_{2} - 4 m + 33 = 1524038 \\ \Leftrightarrow x_{1}^{2} - 2 m x_{1} - 4 m - 5 + 2 (x_{1} + x_{2}) = 1524000 \end{array}$

Do $x_{1}$ là nghiệm của phương trình $(1) \Rightarrow x_{1}^{2} - 2 m x_{1} - 4 m - 5 = 0$

$\Rightarrow 2 (x_{1} + x_{2}) = 1524000 \Leftrightarrow 2.2 m = 1524000 \Leftrightarrow m = 381000$

Vậy $m = 381000$ thỏa mãn yêu cầu bài toán

Câu 8:

Trên nửa đường tròn đường kính AB lấy hai điểm I, Q sao cho I thuộc cung AQ Gọi C là giao điểm hai tia AI và BQ . H là giao điểm của hai dây AQ và BI

a,Chứng minh tứ giác CIHQ nội tiếp

Xem đáp án

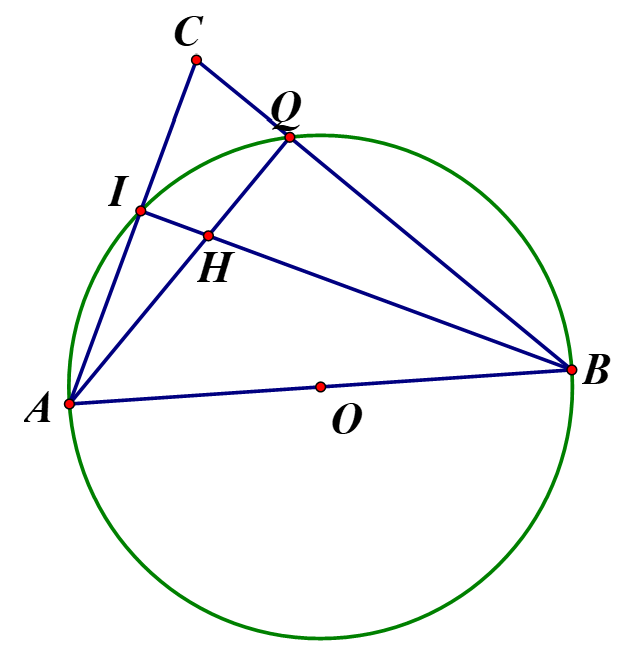
Trên nửa đường tròn đường kính AB lấy hai điểm I, Q sao cho I thuộc cung (ảnh 1)

Ta có: $\hat{A I B} = \hat{A Q B} = 90^{0}$ (góc nội tiếp chắn nửa đường tròn) $\Rightarrow \hat{C I H} = \hat{C Q H} = 90^{0}$

Xét tứ giác $C I H Q$ có $\hat{C I H} + \hat{C Q H} = 90^{0} + 90^{0} = 180^{0} \Rightarrow$ Tứ giác $C I H Q$ là tứ giác nội tiếp (tứ giác có tổng hai góc đối bằng $180^{0})$

Câu 9:

b, Chứng minh $C I . A I = H I . B I$

Xem đáp án

Xét tam giác $A H I$ và tam giác $B C I$ có:

$\hat{A I H} = \hat{B I H} = 90^{0}, \hat{I A H} = \hat{I B C}$ (hai góc nội tiếp cùng chắn cung IQ)

$\Rightarrow Δ A I H ~ Δ B I C (g . g) \Rightarrow \frac{A I}{B I} = \frac{H I}{C I} \Leftrightarrow C I . A I = H I . B I$

Câu 10:

c, Biết $A B = 2 R .$ Tính giá trị của biểu thức $M = A I . A C + B Q . B C$ theo R

Xem đáp án

Ta có: $\begin{array}{l} M = A I . A C + B Q . B C \\ = A C . (A C - I C) + B Q . (B Q + Q C) \\ = A C^{2} - A C . I C + B Q^{2} + B Q . Q C \\ = A Q^{2} + Q C^{2} - A C . I C + B Q^{2} + B Q . Q C \\ = (A Q^{2} + B Q^{2}) + Q C . (Q C + B Q) - A C . I C \\ = A B^{2} + Q C . B C - A C . I C \end{array}$

Tứ giác $A I Q B$ là tứ giác nội tiếp đường tròn (O) $\Rightarrow \hat{C I Q} = \hat{C B A}$ (góc ngoài và góc trong tại đỉnh đối diện của tứ giác nội tiếp)

Xét $Δ C I Q$ và $Δ C B A$ có: $\hat{A C B}$ chung; $\hat{C I Q} = \hat{C B A} (c m t)$

$\Rightarrow Δ C I Q ~ Δ C B A (g . g) \Rightarrow \frac{I C}{B C} = \frac{Q C}{A C} \Rightarrow Q C . B C = A C . I C \Rightarrow Q C . B C - A C . I C = 0$

Vậy $M = A I . A C + B Q . B C = A B^{2} = {(2 R)}^{2} = 4 R^{2}$

Bắt đầu thi ngay

CHỌN BỘ SÁCH BẠN MUỐN XEM

Tổng hợp đề thi chính thức vào 10 môn Toán năm 2019 có đáp án (Phần 1)

Tổng hợp đề thi chính thức vào 10 môn Toán năm 2019 có đáp án (Phần 1)- Đề 5

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm