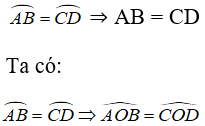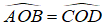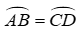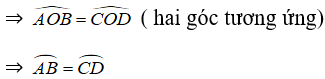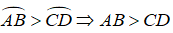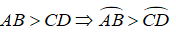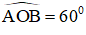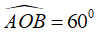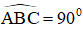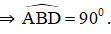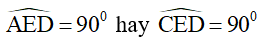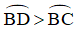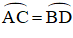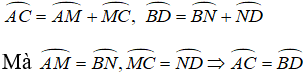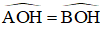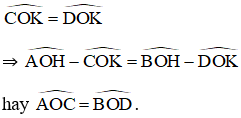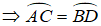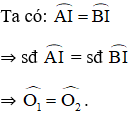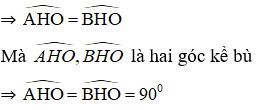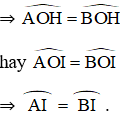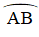Bài 2: Liên hệ giữa cung và dây
-
3532 lượt thi
-
11 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Hãy chứng minh định lý trên.
Xem đáp án
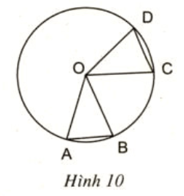
Xét ΔOAB và ΔOCD có:
OA = OC = R
OB = OD = R
⇒ ΔOAB = ΔOCD (c.g.c)
⇒ AB = CD ( hai cạnh tương ứng)
AB = CD ⇒ 
Xét ΔOAB và ΔOCD có:
OA = OC = R
AB = CD (gt)
OB = OD = R
⇒ ΔOAB = ΔOCD (c.c.c)
Câu 3:
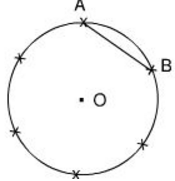
Vẽ đường tròn tâm O, bán kính R = 2cm. Nêu cách vẽ cung AB có số đo bằng 60o. Hỏi dây AB dài bao nhiêu xentimet?
Xem đáp án
+ Dùng compa vẽ đường tròn tâm O, bán kính R = 2cm.
+ Trên đường tròn lấy điểm A.Nối OA từ đó vẽ góc 
Khi đó ta được cung AB có số đo bằng 60º.
+ ΔAOB có OA = OB,
⇒ ΔAOB đều
⇒ AB = OA = OB = R = 2cm.
Câu 4:
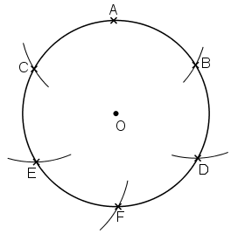
Làm thế nào để chia được đường tròn thành sáu cung bằng nhau như trên hình 12?
Hình 12
Xem đáp án
Chia đường tròn thành 6 cung bằng nhau:
+ Vẽ đường tròn tâm O, bán kính R.
+ Trên đường tròn tâm O, lấy điểm A.
+ Vẽ cung tròn tâm A, bán kính R cắt đường tròn tại B và C.
+ Vẽ cung tròn tâm B và C bán kính R cắt đường tròn tâm O tại giao điểm thứ hai là D và E.
+ Vẽ cung tròn tâm E bán kính R cắt đường tròn (O) tại giao điểm thứ hai là F.
Khi đó, ta chia được đường tròn thành sáu cung bằng nhau như trên
Câu 5:
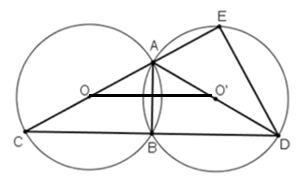
Cho hai đường tròn bằng nhau (O) và (O') cắt nhau tại hai điểm A và B. Kẻ các đường kính AOC, AO'D. Gọi E là giao điểm thứ hai của AC với đường tròn (O').
So sánh các cung nhỏ BC, BD.
Xem đáp án
Vì A,B,C ∈ (O)
⇒ BO = OA = OC
⇒ BO = AC/2.
Tam giác ABC có đường trung tuyến BO và BO bằng một phần hai độ dài cạnh tương ứng AC
=> Tam giác ABC là tam giác vuông tại B ( định lí)
⇒ 
Chứng minh tương tự
Đường tròn tâm O và O’ bằng nhau ⇒ AC = AD.(AC,AD lần lượt là bán kính của (O) và (O’))
Xét hai tam giác vuông ΔABC và ΔABD có:
AB chung, AC = AD
⇒ ΔABC = ΔABD (cạnh huyền – cạnh góc vuông)
⇒ BC = BD(hai cạnh tương ứng)
⇒ 
( định lý )
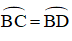
Câu 6:
Cho hai đường tròn bằng nhau (O) và (O') cắt nhau tại hai điểm A và B. Kẻ các đường kính AOC, AO'D. Gọi E là giao điểm thứ hai của AC với đường tròn (O').
Chứng mình rằng B là điểm chính giữa của cung EBD (tức là điểm B chia cung EBD thành hai cung bằng nhau: )
Xem đáp án
Xét tam giác AED có đường trung tuyến EO' bằng một phần hai cạnh tương ứng là AD ( O'E = O'A = O'D = AD/2)
=> Tam giác AED vuông tại E
⇒ 
⇒ ΔECD vuông tại E.
Tam giác ECD vuông có EB là đường trung tuyến ứng với cạnh huyền( Vì BC = BD câu (a) )
⇒ EB = BD (CD/2).
⇒ 
(định lý) hay B là điểm chính giữa cung 
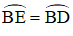
Câu 7:
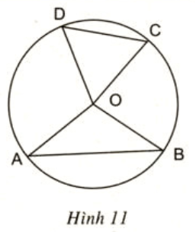
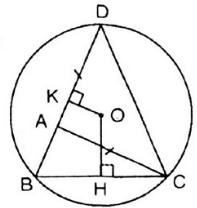
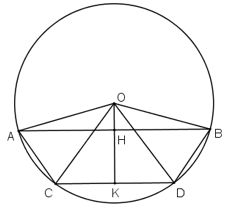
Cho tam giác ABC . Trên tia đối của tia AB lấy một điểm D sao cho AD = AC. Vẽ đường tròn tâm O ngoại tiếp tam giác DBC. Từ O lần lượt hạ các đường vuông góc OH, OK với BC và BD (H ∈ BC, K ∈ BD)
Chứng minh rằng OH > OK.
Xem đáp án
Xét ΔABC có: BC < AB + AC (Bất đẳng thức tam giác)
Mà AD = AC (gt)
⇒ BC < AB + AD = BD
Mà OH là khoảng cách từ O đến dây BC
OK là khoảng cách từ O đến dây BD
⇒ OH > OK.( định lý về khoảng cách từ tâm đến dây)
Câu 8:
Cho tam giác ABC . Trên tia đối của tia AB lấy một điểm D sao cho AD = AC. Vẽ đường tròn tâm O ngoại tiếp tam giác DBC. Từ O lần lượt hạ các đường vuông góc OH, OK với BC và BD (H ∈ BC, K ∈ BD)
So sánh hai cung nhỏ BD và BC
Xem đáp án
Vì BD > BC
⇒ 
Câu 9:
Chứng minh rằng: trong một đường tròn, hai cung bị chắn giữa hai dây song song thì bằng nhau.
Xem đáp án
Vẽ đường tròn tâm O, các dây cung AB // CD.
Cần chứng minh 
Cách 1:
Kẻ bán kính MN // AB // CD
MN // AB
+ TH1: AB và CD cùng nằm trong một nửa đường tròn.
.
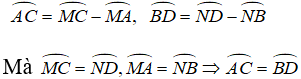
+ TH2: AB và CD thuộc hai nửa đường tròn khác nhau.
Cách 2:
Kẻ OH ⊥ AB; OK ⊥ CD (H ∈ AB, K ∈ CD)
Vì AB // CD ⇒ O, H, K thẳng hàng.
ΔOAB có OA = OB
⇒ ΔOAB cân tại O
⇒ đường cao OH đồng thời là đường phân giác
⇒ 
Chứng minh tương tự:
Câu 10:
Chứng minh rằng đường kính đi qua điểm chính giữa của một cung thì đi qua trung điểm của dây cung căng cung ấy. Mệnh đề đảo có đúng không? Hãy nêu thêm điều kiện để mệnh đề đảo đúng.
Xem đáp án
Vẽ đường tròn tâm O, dây cung AB.
Gọi I là điểm chính giữa của cung AB.
Gọi OI ∩ AB = H.
ΔAOH và ΔBOH có: AO = OB,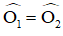 
; OH chung
⇒ ΔAOH = ΔBOH (c-g-c)
⇒ AH = BH (hai cạnh tương ứng)
⇒ OI đi qua trung điểm H của AB.
+ Mệnh đề đảo: Đường kính đi qua trung điểm của một dây cung thì đi qua điểm chính giữa của cung đó.
Mệnh đề sai
Ví dụ: Chọn dây cung AB là một đường kính của (O) (AB đi qua O). Khi đó, tồn tại đường kính CD đi qua O là trung điểm của AB nhưng C,D không phải là điểm chính giữa cung AB ( hình vẽ)
Mệnh đề đảo chỉ đúng khi dây cung AB không phải đường kính.
Câu 11:
Chứng minh rằng đường kính đi qua điểm chính giữa của một cung thì vuông góc với dây cung ấy và ngược lại.
Xem đáp án
+ Cho đường tròn (O); dây cung AB ;
I là điểm chính giữa cung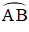 
, H = OI ∩ AB.
⇒ ΔAOH = ΔBOH (cm phần a).
⇒ OH ⊥ AB.
Vậy đường kính đi qua điểm chính giữa của cung thì vuông góc với dây căng cung ấy.
+ Cho đường tròn (O); dây cung AB.
Kẻ đường thẳng OH ⊥ AB (H ∈ AB) cắt đường tròn tại I.
Ta có: ΔABO cân tại O (vì AO = OB = R).
⇒ đường cao OH đồng thời là đường phân giác
⇒ I là điểm chính giữa của cung 
Vậy đường kính vuông góc với dây căng cung thì đi qua điểm chính giữa của cung.
Kiến thức áp dụng