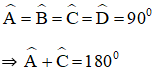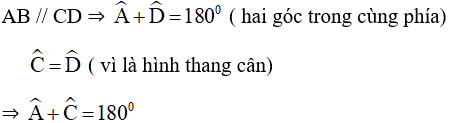6 câu hỏi trắc nghiệm thuộc Luyện tập trang 89-90 - hamchoi.vn

Giải Toán 9 phần Hình học Tập 2

Luyện tập trang 89-90

3531 lượt thi
6 câu hỏi
30 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

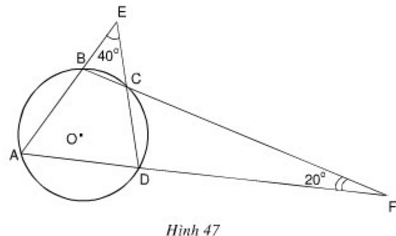
Xem hình 47. Hãy tìm số đo các góc của tứ giác ABCD.

Ta có: $\hat{B C E} = \hat{D C F}$ (hai góc đối đỉnh)

Đặt x = $\hat{B C E} = \hat{D C F}$ . Theotinhs chất góc ngoài tam giác, ta có:

Lại có:

(Hai hóc đối điện tứ giác nội tiếp).

Từ (1),(2),(3) suy ra:

Từ (1), ta có: $\hat{A B C} = 60^{o} + 40^{o} = 100^{o}$

Từ (2), ta có: $\hat{A D C} = 60^{o} + 20^{o} = 80^{o}$

Câu 2:

Trong các hình sau, hình nào nội tiếp được trong một đường tròn:

Hình bình hành, hình chữ nhật, hình vuông, hình thang, hình thang vuông, hình thang cân? Vì sao?

Các hình nội tiếp được trong một đường tròn là:

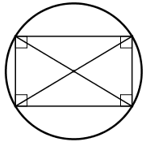
+ Hình chữ nhật:

Hình chữ nhật ABCD có:

⇒ ABCD nội tiếp trong một đường tròn. Đường tròn đó là đường tròn đường kính AC.

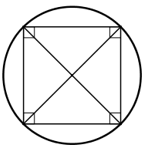
+ Hình vuông:

Vì hình vuông là hình chữ nhật

⇒ Hình vuông cũng nội tiếp trong một đường tròn.

+ Hình thang cân:

Hình thang cân ABCD có:

⇒ ABCD nội tiếp trong một đường tròn.

Câu 3:

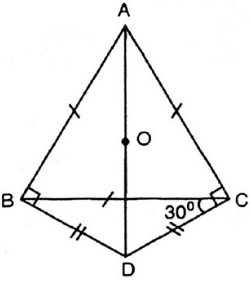
Cho tam giác đều ABC. Trên nửa mặt phẳng bờ BC không chứa đỉnh A, lấy điểm D sao cho DB = DC và $\hat{D C B} = \frac{1}{2} \hat{A C B}$ . Chứng minh tứ giác ABDC là tứ giác nội tiếp.

Do tam giác ABC là tam giác nên $\hat{A C B} = 60^{o}$

=> Tứ giác ABDC có:

=> ABDC là tứ giác nội tiếp

Câu 4:

Cho tam giác đều ABC. Trên nửa mặt phẳng bờ BC không chứa đỉnh A, lấy điểm D sao cho DB = DC và $\hat{D C B} = \frac{1}{2} \hat{A C B}$ . Xác định tâm của đường tròn đi qua bốn điểm A, B, D, C

Ta có: $\hat{A B D} = 90^{o}$

⇒ AD là đường kính của đường tròn ngoại tiếp tam giác ABD Mà ABDC là tứ giác nội tiếp

⇒ AD là đường kính của đường tròn ngoại tiếp tứ giác ABDC.

⇒ tâm O là trung điểm AD.

Vậy tâm đường tròn đi qua bốn điểm A, B, D, C là trung điểm AD.

Câu 5:

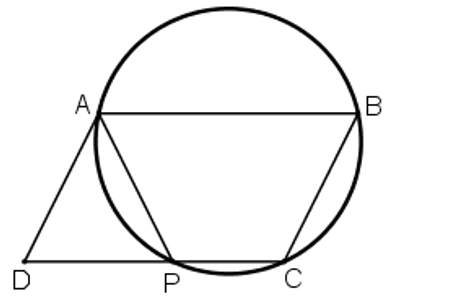
Cho hình bình hành ABCD. Đường tròn đi qua ba đỉnh A, B, C cắt đường thẳng CD tại P khác C. Chứng minh AP = AD.

+ Do ABCD là hình bình hành nên AB//CD

$\Rightarrow \hat{A B C} + \hat{B C P} = 180^{o}$ (hai góc trong cùng phía) (1)

+ ABCP là tứ giác nội tiếp

$\Rightarrow \hat{P A B} + \hat{B C P} = 180^{o} (2)$

Từ (1) và (2) suy ra: $\hat{P A B} = \hat{A B C}$

+ Tứ giác ABCP có: AB//CP (vì AB//CD)

=> Tứ giác ABCP là hình thang.

Lại có: $\hat{P A B} = \hat{A B C}$ nên ABCP là hình thang cân.

=> AP=BC (3)

Mà ABCD là hình bình hành => AD = BC (4)

Từ (3) và (4) suy ra AP=AD (đpcm).

Câu 6:

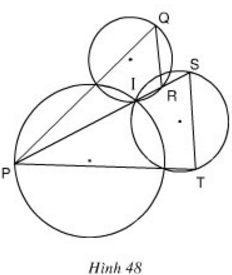
Xem hình 48. Chứng minh QR // ST.

Hướng dẫn: Xét cặp góc so le trong $\hat{P S T}, \hat{S R Q}$

(hai góc kề bù)

Từ (1);(2);(3)

Bắt đầu thi ngay

Bài thi liên quan

Có thể bạn quan tâm