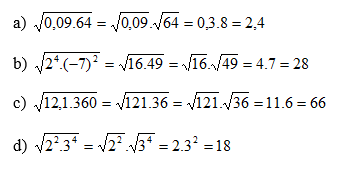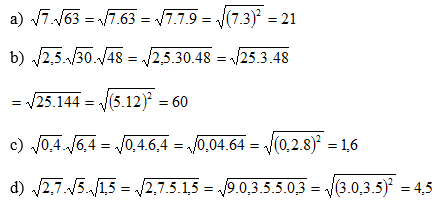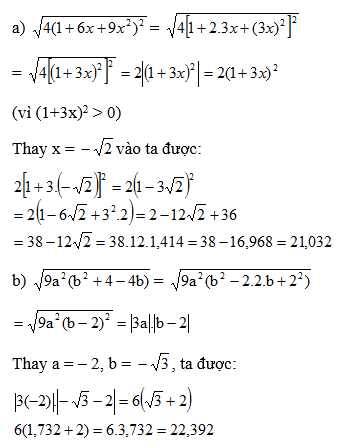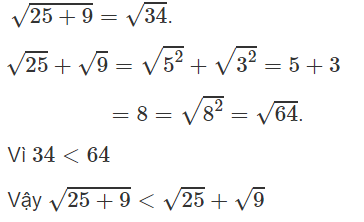14 câu hỏi trắc nghiệm thuộc Bài 3: Liên hệ giữa phép nhân và phép khai phương

Câu 1:

Tính và so sánh: $\sqrt{(16.25)}$ và $\sqrt{16} . \sqrt{25}$

Xem đáp án

$\sqrt{(16.25)} = \sqrt{400} = 20 \sqrt{16} . \sqrt{25} = 4.5 = 20$

Vậy $\sqrt{(16.25)} = \sqrt{16} . \sqrt{25}$

Câu 2:

Tính

a) $\sqrt{(0, 16.0, 64.225)}$

b) $\sqrt{(250.360)}$

Xem đáp án

a) $\sqrt{(0, 16.0, 64.225)}$

$= \sqrt{0, 16} . \sqrt{0, 64} . \sqrt{225}$

$= 0, 4.0, 8.15 = 4, 8$

b) $\sqrt{(250.360)}$

$= \sqrt{25.36.100}$

$= \sqrt{25} . \sqrt{36} . \sqrt{100}$

$= 5.6.10 = 300$ .

Câu 3:

Tính

a) $\sqrt{3} . \sqrt{75};$

b) $\sqrt{20} . \sqrt{72} . \sqrt{(4, 9)}$

Rút gọn các biểu thức sau (với a và b không âm):

a) $\sqrt{(3 a^{3})} . \sqrt{12 a};$

b) $\sqrt{(2 a . 32 a b^{2})}$

Xem đáp án

a) $\sqrt{3} . \sqrt{75} = \sqrt{3.75} = \sqrt{225} = 15$

b) $\sqrt{20} . \sqrt{72} . \sqrt{4, 9} = \sqrt{(20.72.4, 9)} = \sqrt{(2.72.10.4, 9)}$

$= \sqrt{(144.49)} = \sqrt{{(12.7)}^{2}} = 84$

a) $\sqrt{(3 a^{3})} . \sqrt{12 a} = \sqrt{(3 a^{3} . 12 a)} = \sqrt{(36 a^{4})}$

$\sqrt{({(6 a^{2})}^{2})} = 6 a^{2}$ (do $a^{2} \geq 0$ )

b) $\sqrt{(2 a . 32 a b^{2})} = \sqrt{(64 a^{2} b^{2})}$

$\sqrt{({(8 a b)}^{2})} = 8 a b$ (do $a \geq 0; b \geq 0$ )

Câu 4:

Áp dụng quy tắc khai phương một tích, hãy tính:

a) $\sqrt{0, 09.64}$ b) $\sqrt{2^{4} . {(- 7)}^{2}}$

c) $\sqrt{12, 1.360}$ d) $\sqrt{2^{2} . 3^{4}}$

Xem đáp án

Câu 5:

Áp dụng quy tắc nhân các căn bậc hai, hãy tính:

a) $\sqrt{7} . \sqrt{63}$ b) $\sqrt{2, 5} . \sqrt{30} . \sqrt{48}$

c) $\sqrt{0, 4 . \sqrt{6, 4}}$ d) $\sqrt{2, 7} . \sqrt{5} . \sqrt{1, 5}$

Xem đáp án

Câu 6:

Rút gọn các biểu thức sau:

a) $\sqrt{0, 36 a^{2}}$ với $a < 0$

b) $\sqrt{a^{4} . {(3 - a)}^{2}}$ với $a \geq 3$

c) $\sqrt{27.48 . {(1 - a)}^{2}}$ với $a > 1$

d) $\frac{1}{a - b} . \sqrt{a^{4} {(a - b)}^{2}}$ với $a > b$

Xem đáp án

a) $\sqrt{0, 36 a^{2}} = \sqrt{0, 36} . \sqrt{a^{2}} = 0, 6 . |a| = 0, 6 a$ (vì $a < 0$ )

b) $\sqrt{a^{4} {(3 - a)}^{2}} = \sqrt{a^{4}} . \sqrt{{(3 - a)}^{2}} = a^{2} . |3 - a| = a^{2} (a - 3)$

(vì $a \geq 3 \Rightarrow a - 3 \geq 3$ )

c) $\sqrt{27.48 {(1 - a)}^{2}} = \sqrt{9.3.3.16 . {(1 - a)}^{2}}$

$\sqrt{{(9.4)}^{2}} . \sqrt{{(1 - a)}^{2}} = 36 |1 - a| = 36 (a - 1)$

(vì $a > 1 \Rightarrow a - 1 > 0$ )

d) $\frac{1}{a - b} \sqrt{a^{4} {(a - b)}^{2}} = \frac{1}{a - b} . a^{2} |a - b|$

$= \frac{1}{a - b} . a^{2} (a - b) = a^{2}$ (vì $a > b$ nên $a - b > 0$ )

Câu 7:

Rút gọn các biểu thức sau:

a) $\sqrt{\frac{2 a}{3}} . \sqrt{\frac{3 a}{8}}$ với $a \geq 0$

b) $\sqrt{13 a} . \sqrt{\frac{52}{a}}$ với $a > 0$

c) $\sqrt{5 a} . \sqrt{45 a} - 3 a$ với $a \geq 0$

d) ${(3 - a)}^{2} - \sqrt{0, 2} . \sqrt{180 a^{2}}$

Xem đáp án

a) Ta có:

$\sqrt{\frac{2 a}{3}} . \sqrt{\frac{3 a}{8}} = \sqrt{\frac{2 a}{3} . \frac{3 a}{8}} = \sqrt{\frac{2 a . 3 a}{3.8}} = \sqrt{\frac{(2.3) . (a . a)}{3.8}} = \sqrt{\frac{6 a^{2}}{24}} = \sqrt{\frac{6 a^{2}}{6.4}} = \sqrt{\frac{a^{2}}{4}} = \sqrt{\frac{a^{2}}{2^{2}}} = \sqrt{{(\frac{a}{2})}^{2}} = |\frac{a}{2}| = \frac{a}{2} .$

Vì $a \geq 0$ nên $\frac{a}{2} \geq 0 \Rightarrow |\frac{a}{2}| = \frac{a}{2} .$

b) Ta có:

$\sqrt{13 a} . \sqrt{\frac{52}{a}} = \sqrt{13 a . \frac{52}{a}} = \sqrt{\frac{13 a . 52}{a}} = \sqrt{\frac{13 a . (13.4)}{a}} = \sqrt{\frac{(13.13) . 4 . a}{a}} = \sqrt{13^{2} . 4} = \sqrt{13^{2}} . \sqrt{4} = \sqrt{13^{2}} . \sqrt{2^{2}} = 13.2 = 26$

c) Do $a \geq 0$ nên bài toán luôn xác định.Ta có:

$\sqrt{5 a} . \sqrt{45 a} - 3 a = \sqrt{5 a . 45 a} - 3 a = \sqrt{(5 . a) . (5.9 . a)} - 3 a = \sqrt{(5.5) . 9 . (a . a)} - 3 a = \sqrt{5^{2} . 3^{2} . a^{2}} - 3 a = \sqrt{5^{2}} . \sqrt{3^{2}} . \sqrt{a^{2}} - 3 a = 5.3 . |a| - 3 a = 15 |a| - 3 a = 15 a - 3 a = (15 - 3) a = 12 a .$

(Vì $a \geq 0$ nên $|a| = a$ )

d) Ta có

${(3 - a)}^{2} - \sqrt{0, 2} . \sqrt{180 a^{2}} = \sqrt{0, 2.180 a^{2}} = {(3 - a)}^{2} - \sqrt{0, 2 . (10.18) . a^{2}} = {(3 - a)}^{2} - \sqrt{(0, 2.10) . 18 . a^{2}} = {(3 - a)}^{2} - \sqrt{2.18 . a^{2}} = {(3 - a)}^{2} - \sqrt{36 a^{2}} = {(3 - a)}^{2} - \sqrt{36} . \sqrt{a^{2}} = {(3 - a)}^{2} - \sqrt{6^{2}} . \sqrt{a^{2}} = {(3 - a)}^{2} - 6 . |a| .$

+) TH1: Nếu $a \geq 0 \Rightarrow |a| = a .$

Do đó : ${(3 - a)}^{2} - 6 |a| = {(3 - a)}^{2} - 6 a$

$= (3^{2} - 2.3 . a + a^{2}) - 6 a = (9 - 6 a + a^{2}) - 6 a = 9 - 6 a + a^{2} - 6 a = a^{2} + (- 6 a - 6 a) + 9 = a^{2} + (- 12 a) + 9 = a^{2} - 12 a + 9 .$

+TH2: Nếu $a < 0 \Rightarrow |a| = - a .$

Do đó : ${(3 - a)}^{2} - 6 |a| = {(3 - a)}^{2} - 6 . (- a)$

$= (3^{2} - 2.3 . a + a^{2}) - (- 6 a) = (9 - 6 a + a^{2}) + 6 a = 9 - 6 a + a^{2} + 6 a = a^{2} + (- 6 a + 6 a) + 9 = a^{2} + 9 .$

Vậy ${(3 - a)}^{2} - \sqrt{0, 2} . \sqrt{180 a^{2}} = a^{2} - 12 a + 9$ nếu $a \geq 0$

${(3 - a)}^{2} - \sqrt{0, 2} . \sqrt{180 a^{2}} = a^{2} + 9$ nếu $a < 0 .$

Câu 8:

Khai phương tích 12.30.40 được:

(A) 1200 ; (B) 120 ; (C) 12 ; (D) 240

Hãy chọn kết quả đúng.

Xem đáp án

- Chọn B

- Vì ta có:

$\sqrt{12.30.40} = \sqrt{36.400} = \sqrt{{(6.20)}^{2}} = 120$ .

Câu 9:

Biến đổi các biểu thức dưới dấu căn thành dạng tích rồi tính:

a) $\sqrt{13^{2} - 12^{2}}$ b) $\sqrt{17^{2} - 8^{2}}$

c) $\sqrt{117^{2} - 108^{2}}$ d) $\sqrt{313^{2} - 312^{2}}$

Xem đáp án

a) $\sqrt{13^{2} - 12^{2}} = \sqrt{(13 - 12) (13 + 12)}$

$= \sqrt{1.25} = 5$

b) $\sqrt{17^{2} - 8^{2}} = \sqrt{(17 - 8) (17 + 8)}$

$= \sqrt{9.25} = 3.5 = 15$

c) $\sqrt{117^{2} - 108^{2}} = \sqrt{(117 - 108) (117 + 108)}$

$\sqrt{9.225} = \sqrt{9} . \sqrt{225} = 3.15 = 45$

d) $\sqrt{313^{2} - 312^{2}} = \sqrt{(313 - 312) (313 + 312)}$

$= \sqrt{1.625} = \sqrt{25^{2}} = 25$ .

Câu 10:

Chứng minh:

a) $(2 - \sqrt{3}) (2 + \sqrt{3}) = 1$

b) $(\sqrt{2006} - \sqrt{2005})$ và $(\sqrt{2006} + \sqrt{2005})$

là hai số nghịch đảo của nhau.

Xem đáp án

Câu 11:

Rút gọn và tìm giá trị (làm tròn đến chữ số thập phân thứ ba) của các căn thức sau:

a) $\sqrt{4 {(1 + 6 x + 9 x^{2})}^{2}}$ tại $x = - \sqrt{2}$

b) $\sqrt{9 a^{2} (b^{2} + 4 - 4 b)}$ tại $a = - 2, b = - \sqrt{3}$

Xem đáp án

Câu 12:

Tìm x, biết:

a) $\sqrt{16 x} = 8$ b) $\sqrt{4 x} = \sqrt{5}$

c) $\sqrt{9 (x - 1)} = 21$ d) $\sqrt{4 {(1 - x)}^{2}} - 6 = 0$

Xem đáp án

a) $\sqrt{16 x} = 8$ (điều kiện: $x \geq 0$ )

$\Leftrightarrow 16 x = 82 \Leftrightarrow 16 x = 64 \Leftrightarrow x = 4$

(Hoặc: $\sqrt{16 x} = 8 \Leftrightarrow \sqrt{16} . \sqrt{x} = 8$

$\Leftrightarrow 4 \sqrt{x} = 8 \Leftrightarrow \sqrt{x} = 2 \Leftrightarrow x = 4)$

b) Điều kiện $x \geq 0$

$\sqrt{4 x} = \sqrt{5} \Leftrightarrow 4 x = 5 \Leftrightarrow x = \frac{5}{4} \Leftrightarrow x = 1, 25$

c) Điều kiện $x - 1 \geq 0 \Leftrightarrow x \geq 1$ (*)

$\sqrt{9 (x - 1)} = 21 \Leftrightarrow \sqrt{9} . \sqrt{x - 1} = 21 \Leftrightarrow 3 \sqrt{x - 1} = 21$

$\Leftrightarrow \sqrt{x - 1} = 7 \Leftrightarrow x - 1 = 49 \Leftrightarrow x = 50$

Cách khác:

$\sqrt{9 (x - 1)} = 21 \Leftrightarrow 9 (x - 1) = 21^{2} \Leftrightarrow 9 (x - 1) = 441$

$x - 1 = 49 \Leftrightarrow x = 50$

$x = 50$ thỏa mãn điều kiện (*) nên $x = 50$ là nghiệm của phương trình.

d) Vì ${(1 - x)}^{2} \geq 0 \forall x$ nên phương trình xác định với mọi giá trị của x.

$\sqrt{4 {(1 - x)}^{2}} - 6 = 0 \Leftrightarrow \sqrt{4 {(1 - x)}^{2}} = 6 \Leftrightarrow 2 |1 - x| = 6$

Khi 1 – x ≥ 0 ⇔ x ≤ 1

Ta có: 2|1 – x| = 6 ⇔ 2(1 – x) = 6 ⇔ 2(1 – x) = 6

⇔ –2x = 4 ⇔ x = –2 (nhận)

- Khi 1 – x < 0 ⇔ x > 1

Ta có: 2|1 – x| = 6 ⇔ 2[– (1 – x)] = 6

⇔ x – 1 = 3 ⇔ x = 4 (nhận)

Vậy phương trình có hai nghiệm: x = - 2; x = 4

Câu 13:

So sánh :

a) So sánh $\sqrt{25 + 9}$ và $\sqrt{25} + \sqrt{9}$

b) Với $a > 0$ và $b > 0$ , chứng minh $\sqrt{a + b} < \sqrt{a} + \sqrt{b}$

Xem đáp án

a) Ta có:

b) Ta có:

Câu 14:

So sánh:

a) 4 và $2 \sqrt{3}$ ; b) $- \sqrt{5}$ và $- 2$

Xem đáp án

a) Ta có: $2 = \sqrt{4} > \sqrt{3}$ nên $2.2 > 2 \sqrt{3}$

Vậy $\sqrt{4} > 2 \sqrt{3}$

b) Ta có: $\sqrt{5} > \sqrt{4} = 2$ nên $\sqrt{5} > 2$

Vậy $- \sqrt{5} < - 2$

CHỌN BỘ SÁCH BẠN MUỐN XEM

Giải SGK Toán 9 Chương 1: Căn bậc hai. Căn bậc ba

Bài 3: Liên hệ giữa phép nhân và phép khai phương

Danh sách câu hỏi

Bài thi liên quan

Các bài thi hot trong chương