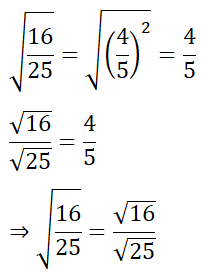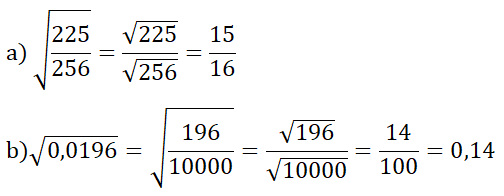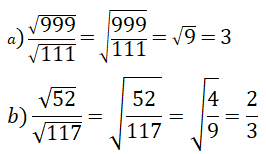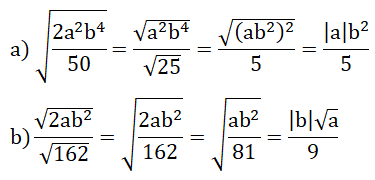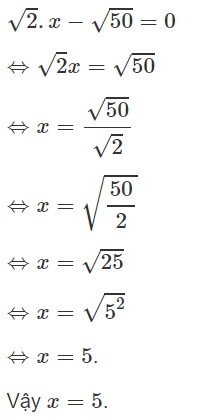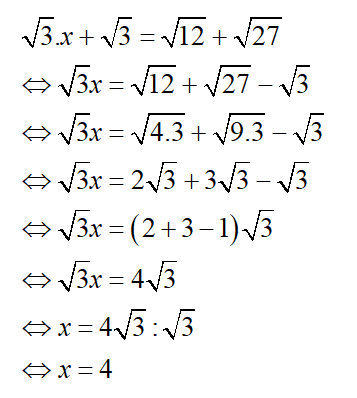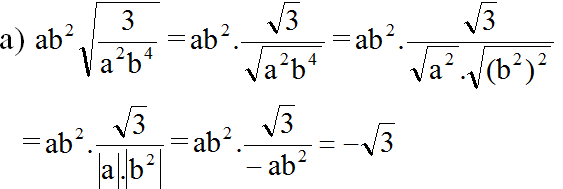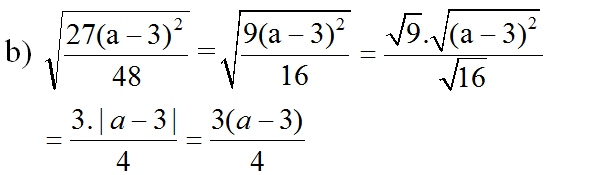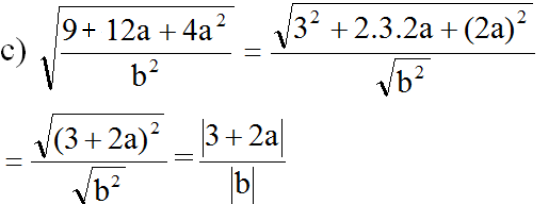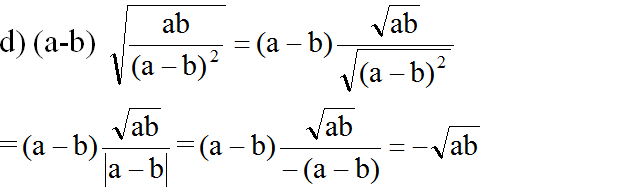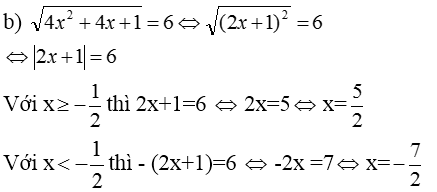13 câu hỏi trắc nghiệm thuộc Bài 4: Liên hệ giữa phép chia và phép khai phương

Câu 1:

Tính và so sánh

$\sqrt{\frac{16}{25}}$ và $\frac{\sqrt{16}}{\sqrt{25}}$

Xem đáp án

Câu 2:

Tính

a) $\sqrt{\frac{225}{256}}$

b) $\sqrt{0, 0196}$

Xem đáp án

Câu 3:

Tính:

a) $\frac{\sqrt{999}}{\sqrt{111}}$ b) $\frac{\sqrt{52}}{\sqrt{117}}$

Rút gọn:

a) $\sqrt{\frac{2 a^{2} b^{4}}{50}}$ b) $\frac{\sqrt{2 a b^{2}}}{\sqrt{162}}$ với $a \geq 0$

Xem đáp án

Câu 4:

Tính:

a) $\sqrt{\frac{289}{225}}$ b) $\sqrt{2 \frac{14}{25}}$

c) $\sqrt{\frac{0, 25}{9}}$ c) $\sqrt{\frac{8, 1}{1, 6}}$

Xem đáp án

Câu 5:

Tính:

a) $\frac{\sqrt{2}}{\sqrt{18}}$ b) $\frac{\sqrt{15}}{\sqrt{735}}$

c) $\frac{\sqrt{12500}}{\sqrt{500}}$ d) $\frac{\sqrt{6^{5}}}{\sqrt{2^{3} . 3^{5}}}$

Xem đáp án

Câu 6:

Rút gọn các biểu thức sau:

a) $\frac{y}{x} . \sqrt{\frac{x^{2}}{y^{4}}}$ với $x > 0, y \neq 0$

b) $\frac{y}{x} . \sqrt{\frac{x^{2}}{y^{4}}}$ với $y < 0$

c) $5 x y . \sqrt{\frac{25 x^{2}}{y^{6}}}$ với $x < 0, y > 0$

d) $0, 2 x^{3} y^{3} \sqrt{\frac{16}{x^{4} y^{8}}}$ với $x \neq 0, y \neq 0$

Xem đáp án

a) $\frac{y}{x} . \sqrt{\frac{x^{2}}{y^{4}}} = \frac{y}{x} . \sqrt{\frac{x^{2}}{y^{4}}} = \frac{y}{x} . \frac{|x|}{|y^{2}|} = \frac{y}{x} . \frac{x}{y^{2}} = \frac{1}{y}$

(Vì $x > 0$ nên $|x| = x; y^{2} > 0$ với mọi $y \neq 0$ )

b) $2 y^{2} . \sqrt{\frac{x^{4}}{4 y^{2}}} = 2 y^{2} . \frac{|x^{2}|}{|2 y|} = 2 y^{2} . \frac{x^{2}}{- 2 y} = - x^{2} y$

(Vì $x^{2} \geq 0$ với mọi x; và vì $y < 0$ nên $|2 y| = - 2 y$ )

c) $5 x y . \sqrt{\frac{25 x^{2}}{y^{6}}} = 5 x y . \frac{|5 x|}{|y^{3}|} = 5 x y . \frac{- 5 x}{y^{3}} = - \frac{25 x^{2}}{y^{2}}$

(Vì $x < 0$ nên $|5 x| = - 5 x; y > 0$ nên $|y^{3}| = y^{3}$ )

d) $0, 2 x^{3} . y^{3} . \sqrt{\frac{16}{x^{4} y^{8}}} = 0, 2 x^{3} y^{3} . \frac{\sqrt{16}}{\sqrt{x^{4} . y^{8}}}$

$0, 2 . x^{3} y^{3} . \frac{4}{|x^{2} y^{4}|} = \frac{0, 8 x}{y}$

( Vì $x^{2} y^{4} = {(x y^{2})}^{2} > 0$ với mọi $x \neq 0, y \neq 0$ )

Câu 7:

a) So sánh $\sqrt{25 - 16}$ và $\sqrt{25} - \sqrt{16}$

b) Chứng minh rằng ,với $a > b > 0$ thì

$\sqrt{a} - \sqrt{b} < \sqrt{a - b}$

Xem đáp án

a) $\sqrt{25 - 16} = \sqrt{9} = \sqrt{3^{2}} = 3$

$\sqrt{25} - \sqrt{16} = \sqrt{5^{2}} - \sqrt{4^{2}} = 5 - 4 = 1$

Vì $3 > 1$ nên $\sqrt{25 - 16} > \sqrt{25} - \sqrt{16}$

b) Với $a > b > 0$ để chứng minh $\sqrt{a} - \sqrt{b} < \sqrt{a - b}$

ta quy về so sánh $\sqrt{a}$ với $\sqrt{a - b} + \sqrt{b}$ .

Áp dụng kết quả bài 26,với hai số (a-b) và b ta sẽ được

$\sqrt{a - b} + \sqrt{b} > \sqrt{a - b + b}$ hay $\sqrt{a - b} + \sqrt{b} > \sqrt{a} .$

Vậy $\sqrt{a - b} > \sqrt{a} - \sqrt{b}$ .

Câu 8:

Tính:

a) $\sqrt{1 \frac{9}{16} . 5 \frac{4}{9} . 0, 01}$

b) $\sqrt{1, 44.1, 21 - 1, 44.0, 4}$

c) $\sqrt{\frac{165^{2} - 124^{2}}{164}}$

d) $\sqrt{\frac{149^{2} - 76^{2}}{457^{2} - 384^{2}}}$

Xem đáp án

Câu 9:

Giải phương trình:

a) $\sqrt{2} . x - \sqrt{50} = 0$

b) $\sqrt{3} . x + \sqrt{3} = \sqrt{12} + \sqrt{27}$

c) $\sqrt{3} . x^{2} - \sqrt{12} = 0$

d) $\frac{x^{2}}{\sqrt{5}} - \sqrt{20} = 0$

Xem đáp án

a)

b)

c)

d)

Câu 10:

Rút gọn các biểu thức sau:

a) $a b^{2} . \sqrt{\frac{3}{a^{2} b^{4}}}$ với $a < 0, b \neq 0$

b) $\sqrt{\frac{27 {(a - 3)}^{2}}{48}}$ với $a > 3$

c) $\sqrt{\frac{9 + 12 a + 4 a^{2}}{b^{2}}}$ với $a \geq - 1, 5$ và $b < 0$

d) $(a - b) . \sqrt{\frac{a b}{{(a - b)}^{2}}}$ với $a < b < 0$

Xem đáp án

(vì a < 0 nên |a| = -a, $b^{2} > 0$ với mọi b ≠ 0 nên $|b^{2}| = b^{2}$ )

(vì a > 3 nên |a - 3| = a - 3)

Vì b < 0 nên |b| = -b

Vì a ≥ -1,5 nên 3 + 2a ≥ 0. Do đó: |3 + 2a| = 3 + 2a

Vậy:

(vì a < b < 0 và b < 0 nên |a - b| = -(a - b), ab > 0)

Câu 11:

Tìm x, biết:

a) $\sqrt{{(x - 3)}^{2}} = 9$

b) $\sqrt{4 x^{2} + 4 x + 1} = 6$

Xem đáp án

- Với x ≥ 3 thì |x - 3| = x - 3 nên ta được:

x - 3 = 9 ⇔ x = 12

- Với x < 3 thì |x - 3| = 3 - x nên ta được:

3 - x = 9 ⇔ x = -6

Vậy phương trình có hai nghiệm: x = 12; x = -6

Câu 12:

Mỗi khẳng định sau đúng hay sai? Vì sao?

a) $0, 01 = \sqrt{0, 0001}$

b) $- 0, 5 = \sqrt{- 0, 25}$

c) $\sqrt{39} < 7$ và $\sqrt{39} > 6$

d) $(4 - \sqrt{3}) . 2 x < \sqrt{3} (4 - \sqrt{13}) \Leftrightarrow < \sqrt{13}$

Xem đáp án

a) Đúng, vì $\sqrt{0, 0001} = \sqrt{0, 01^{2}} = 0, 01$

b) Sai, vì vế phải không có nghĩa.

(Lưu ý: $\sqrt{A}$ có nghĩa khi A ≥ 0)

c) Đúng, vì $7 = \sqrt{7^{2}} = \sqrt{49} > \sqrt{39}$

$6 = \sqrt{6^{2}} = \sqrt{36} < \sqrt{39}$

d) Đúng, vì $4 - \sqrt{13} = \sqrt{4^{2}} - \sqrt{13} = \sqrt{16} - \sqrt{13} > 0$

Do đó: $(4 - \sqrt{13}) . 2 x < \sqrt{3} (4 - \sqrt{13})$ (giản ước hai vế với $(4 - \sqrt{13})$ )

$\Leftrightarrow 2 x < \sqrt{3}$

Câu 13:

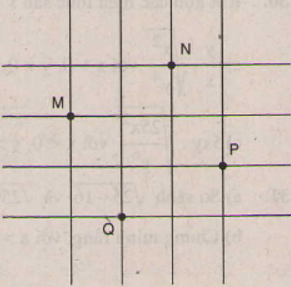
Đố. Trên lưới ô vuông, mỗi ô cạnh 1cm, cho bốn điểm M, N, P, Q. Hãy xác định số đô cạnh, đường chéo và diện tích của tứ giác MNPQ.

Hình 3

Xem đáp án

Dựa vào định lý Pitago, ta thấy mỗi cạnh của tứ giác MNPQ là đường chéo của hình chữ nhật do hai ô vuông ghép lại, nên hình đó có bốn cạnh bằng nhau và bằng

Tứ giác MNPQ là hình thoi có bốn cạnh bằng nhau.

Mỗi đường chéo của tứ giác MNPQ là đường chéo của hình chữ nhật do ba ô vuông ghép lại, nên giác NMPQ có hai đường chéo bằng nhau và bằng

Hình thoi MNPQ là hình vuông có hai đường chéo bằng nhau.

Diện tích hình vuông MNPQ:

S = ${(\sqrt{5})}^{2} = 5 (c m^{2})$

CHỌN BỘ SÁCH BẠN MUỐN XEM

Giải SGK Toán 9 Chương 1: Căn bậc hai. Căn bậc ba

Bài 4: Liên hệ giữa phép chia và phép khai phương

Danh sách câu hỏi

Bài thi liên quan

Các bài thi hot trong chương