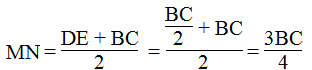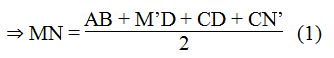17 câu hỏi trắc nghiệm thuộc Bài 4: Toán 8 Đường trung bình của tam giác, của hình thang

Câu 1:

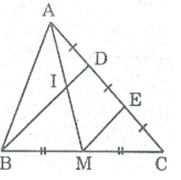
Cho tam giác ABC, điểm D thuộc cạnh AC sao cho AD = $\frac{1}{2}$ DC, Gọi M là trung điểm của BC, I là giao điểm của BD và AM. Chứng minh: AI = IM

Xem đáp án

Gọi E là trung điểm của DC

Trong ΔBDC, ta có:

M là trung điểm của BC (gt)

E là trung điểm của CD (gt)

Nên ME là đường trung bình của $∆$ BCD

⇒ME // BD (tính chất đường trung bình tam giác)

Ta có: AD = $\frac{1}{2}$ DC (gt)

DE = $\frac{1}{2}$ DC (cách vẽ)

⇒ AD = DE. Do đó D là trung điểm của AE

Xét ∆AEM, có:

D là trung điểm của AE

DI//ME

⇒ I là trung điểm của AM hay AI = IM.

Câu 2:

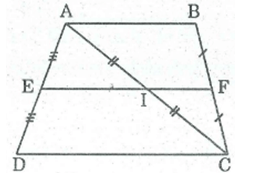
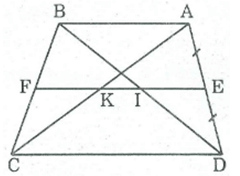
Hình thang ABCD có đáy AB, CD. Gọi E, F, I theo thứ tự là trung điểm của AD, BC, AC. Chứng minh rằng ba điểm E, F, I thắng hàng.

Xem đáp án

* Hình thang ABCD có AB // CD

E là trung điểm của AD (gt)

F là trung điểm của BC (gt)

Nên EF là đường trung bình của hình thang ABCD

EF // CD (tỉnh chất đưòng trung bình hình thang) (1)

* Trong $∆$ ADC ta có:

E là trung điểm của AD (gt)

I là trung điểm của AC (gt)

Nên EI là đường trung bình của $∆$ ADC

⇒ EI // CD (tính chất đường trung bình tam giác) (2)

Từ (1) và (2) và theo tiên đề ƠClít ta có đường thẳng EF và EI trùng nhau. Vậy E, F, I thẳng hàng

Câu 3:

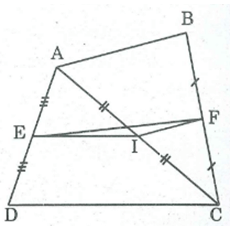
Cho tứ giác ABCD. Gọi E, F, I theo thứ tự là trung đếm của AD, BC, AC. Chứng minh rằng: EI//CD, IF//AB

Xem đáp án

* Trong tam giác ADC, ta có:

E là trung điểm của AD (gt)

I là trung điểm của AC (gt)

Nên EI là đường trung bình của $∆$ ADC

⇒EI // CD (tỉnh chất đường trung bình của tam giác) và EI = CD / 2

* Trong tam giác ABC, ta có:

I là trung điểm của AC

F là trung điểm của BC

Nên IF là đường trung bình của $∆$ ABC

⇒IF // AB (tỉnh chất đường trung bình của tam giác) và IF= AB / 2

Câu 4:

Cho tứ giác ABCD. Gọi E, F, I theo thứ tự là trung đếm của AD, BC, AC. Chứng minh rằng: $E F \leq \frac{A B + C D}{2}$

Xem đáp án

Với 3 điểm E,I,F bất kì ta có: EF ≤ EI + IF (dấu “ = ” xảy ra khi I nằm giữa E và F) mà EI = CD / 2 ; IF= AB / 2 (chứng minh trên)

⇒ $E F \leq \frac{C D}{2} + \frac{A B}{2}$

Vậy $E F \leq \frac{A B + C D}{2}$ (dấu bằng xảy ra khi AB // CD)

Câu 5:

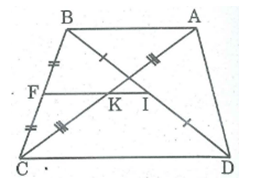
Cho hình thang ABCD (AB // CD), M là trung điểm của AD, N là trung điểm của BC. Gọi I, K theo thứ tự là giao điểm của MN với BD, AC. Cho biết AB = 6cm, CD = l4cm. Tính độ dài MI, IK, KN.

Xem đáp án

Hình thang ABCD có AB // CD

M là trung điểm của AD (gt)

N là trung điểm của BC (gt)

Nên MN là đường trung bình của hình thang ABCD ⇒ MN//AB// CD

MN = (AB + CD) / 2 = (6 + 14) / 2 = 10 (cm)

* Trong tam giác ADC, ta có:

M là trung điểm của AD

MK // CD

⇒ AK= KC và MK là đường trung bình của $∆$ ADC.

⇒ MK = 1/2 CD = 1/2 .14= 7 (cm)

Vậy: KN = MN – MK = 10 – 7 = 3 (cm)

* Trong $∆$ ADB, ta có:

M là trung điểm của AD

MI // AB nên DI = IB

⇒ MI là đường trung bình của $∆$ DAB

⇒ MI = 1/2 AB = 1/2 .6 = 3 (cm)

IK = MK – Ml = 7 – 3 = 4 (cm)

Câu 6:

Cho tam giác ABC, các đường trung tuyến BD và CE cắt nhau ở G. Gọi I, K theo thứ tự là trung điểm của GB, GC. Chứng minh rằng DE//IK, DE= IK.

Xem đáp án

* Trong $∆$ ABC, ta có:

E là trung điểm của AB (gt)

D là trung điểm của AC (gt)

Nên ED là đường trung bình của $∆$ ABC

⇒ ED//BC và ED = BC/2 (tính chất đường trung bình của tam giác) (l)

* Trong $∆$ GBC, ta có:

I là trung điểm của BG (gt)

K là trúng điểm của CG (gt)

Nên IK là đường trung bình của $∆$ GBC

⇒ IK // BC và IK = BC/2 (tỉnh chất đường trung bình của tam giác) (2)

Từ (l) và (2) suy ra: IK // DE, IK = DE.

Câu 7:

Cho tam giác ABC, đường trung tuyến AM. Gọi D là trung điểm của AM, E là giao điểm của BD và AC. Chứng minh AE = $\frac{1}{2}$ EC

Xem đáp án

Gọi F là trung điểm của EC.

Trong $∆$ CBE, ta có:

M là trung điểm của CB;

F là trung điểm của CE.

Nên MF là đường trung bình của $∆$ CBE

⇒ MF// BE (tính chất đường trung bình của tam giác) hay DE// MF

* Trong $∆$ AMF, ta có: D là trung điểm của AM

DE // MF

Suy ra: AE = EF (tính chất đường trung bình của tam giác)

Mà EF = FC = $\frac{1}{2}$ EC nên AE = $\frac{1}{2}$ EC

Câu 8:

Cho tam giác ABC, các đường trung tuyến BD, CE. Gọi M, N theo thứ tự là trung điểm của BE, CD. Gọi I, K theo thứ tự là giao điểm của MN với BD, CE. Chứng minh MI = IK = KN.

Xem đáp án

Trong $∆$ ABC ta có: E là trung điểm của cạnh AB

D là trung điểm của cạnh AC

Nên ED là đường trung bình của $∆$ ABC

⇒ ED // BC và ED = 1/2 BC

(tính chất đường trung bình của tam giác)

+) Tứ giác BCDE có ED // BC nên BCDE là hình thang.

Trong hình thang BCDE, ta có: BC // DE

M là trung điểm cạnh bên BE

N là trung điểm cạnh bên CD

Nên MN là đường trung hình hình thang BCDE ⇒ MN // DE

(tính chất đường trung bình hình thang)

Trong $∆$ BED, ta có: M là trung điểm BE

MI // DE

Suy ra: MI là đường trung bình của $∆$ BED

⇒ MI = 1/2 DE = 1/4 BC (tính chất đường trung bình của tam giác)

Trong $∆$ CED ta có: N là trung điểm CD

NK // DE

Suy ra: NK là đường trung bình của $∆$ CED

⇒ NK = 1/2 DE = 1/4 BC (tính chất đường trung bình của tam giác)

IK = MN – (MI + NK) = 3/4 BC – (1/4 BC + 1/4 BC) = 1/4 BC

⇒ MI = IK = KN = 1/4 BC

Câu 9:

Chứng minh rằng đường thẳng đi qua trung điểm một cạnh bên của hình thang và song song với hai đáy thì đi qua trung điểm của hai đường chéo và đi qua trung điểm của cạnh bên thứ hai.

Xem đáp án

Xét hình thang ABCD có AB // CD.

E là trung điểm AD, đường thẳng đi qua E song song với AB cắt BC tại F, AC tại K, BD tại I.

Vì E là trung điểm AD nên EF// AB

Suy ra: BF = FC (tính chất đường trung bình hình thang)

Trong $∆$ ADC ta có: E là trung, điểm của cạnh AD

EK // DC

Suy ra: AK = KC (tính chất đường trung bình của tam giác)

Trong $∆$ ABD ta có: E là trung điểm của cạnh AD

EI // AB

Suy ra: BI = ID (tính chất đường trung bình của tam giác)

Vậy đường thẳng song song với 2 đáy, đi qua trung điểm E của cạnh bên AD của hình thang ABCD thì đi qua trung điểm của cạnh bên BC và trung điểm hai đường chéo AC, BD.

Câu 10:

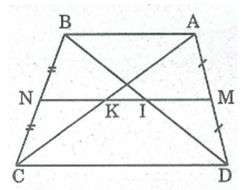
Chứng minh rằng trong hình thang mà hai đáy không bằng nhau, đoạn thẳng nối trung điểm hai đường chéo bằng nửa hiệu của hai đáy.

Xem đáp án

Giả sử hình thang ABCD có AB // CD, AB < CD

Gọi I, K lần lượt là trung điểm hai đường chéo BD, AC; F là trung điểm của BC.

* Trong $∆$ ACB, ta có:

K là trung điểm của cạnh AC

F là trung điểm của cạnh BC

Nên KF là đường trung bình của $∆$ ACB

⇒ KF // AB và KF = 1/2 AB

(tính chất đường trung bình của tam giác)

Trong $∆$ BDC, ta có: I là trung điểm của cạnh BD

F là trung điểm của cạnh BC

Nên IF là đường trung bình của $∆$ BDC

⇒ IF // CD và IF = 1/2 CD (tính chất đường trung bình của tam giác)

FK // AB mà AB // CD nên FK // CD

FI // CD (chứng minh trên)

Suy ra hai đường thẳng FI và FK trùng nhau.

⇒ I, K, F thẳng hàng, AB < CD ⇒ FK < FI nên K nằm giữa I và F

IF = IK + KF

⇒ IK = IF – KF = 1/2 CD - 1/2 AB = (CD - AB)/2

Câu 11:

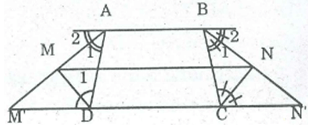
Hình thang ABCD có AB // CD; AB = a, BC = b, CD = c, DA = d. Các đường phân giác của góc ngoài đỉnh A và D cắt nhau tại M, các đường phân giác của các góc ngoài đỉnh B và C cắt nhau tại N. Chứng minh rằng MN // CD

Xem đáp án

Gọi M' và N' là giao điểm của tia AM và BN với CD.

Ta có: $∠$ (M') = $∠ A_{2}$ (sole trong)

$∠ A_{1}$ = $∠ A_{2}$ (gt)

⇒ $∠$ (M') = $∠ A_{1}$ nên $∆$ ADM' cân tại D

* DM là phân giác của $∠$ (ADM' )

Suy ra: DM là đường trung tuyến (tính chất tam giác cân)

⇒ AM = MM'

$∠$ (N') = $∠ B_{1}$ nên $∆$ BCN' cân tại C.

* CN là phân giác của $∠$ (BCN')

Suy ra: CN là đường trung tuyến (tính chất tam giác cân)

⇒ BN = NN'

Suy ra: MN là đường trung bình của hình thang ABN'M'

⇒ MN // M'N' (tính chất đường trung hình hình thang)

Hay MN//CD

Câu 12:

Hình thang ABCD có AB // CD; AB = a, BC = b, CD = c, DA = d. Các đường phân giác của góc ngoài đỉnh A và D cắt nhau tại M, các đường phân giác của các góc ngoài đỉnh B và C cắt nhau tại N. Tính độ dài MN theo a, b, c, d (a. b, c, d có cùng đơn vị đo)

Xem đáp án

MN = (AB + M’N') / 2 (tính chất đường trung hình hình thang)

Mà M'D = AD, CN' = BC.

Thay vào (1) :

Câu 13:

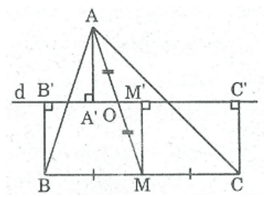
Cho tam giác ABC, đường trung tuyến AM. Gọi 0 là trung điểm của AM. Qua O kẻ đường thẳng d cắt các cạnh AB, AC. Gọi AA', BB', CC' là các đường vuông góc kể từ A, B, C đến đường thẳng d.

Chứng minh rằng: AA' = (BB' + CC') / 2

Xem đáp án

Ta có: BB' ⊥ d (gt)

CC' ⊥ d (gt)

Suy ra: BB'// CC'

Tứ giác BB'C'C là hình thang

Kẻ MM' ⊥ d ⇒ MM' // BB' // CC'

Lại có M là trung điểm của BC nên M' là trung điểm của B’C’

⇒ MM' là đường trung bình của hình thang BB'C'C

⇒ MM' = (BB' + CC') / 2 (1)

* Xét hai tam giác vuông AA'O và MM'O:

$∠$ (AA'O) = $∠$ (MM' O) = $90^{0}$

AO=MO (gt)

$∠$ (AOA') = $∠$ (MOM' ) (2 góc đối đỉnh)

Do đó: $∆$ AA'O = $∆$ MM'O (cạnh huyền, cạnh góc nhọn)

⇒AA' = MM' (2)

Từ (1) và (2) suy ra: AA' = (BB' + CC') / 2

Câu 14:

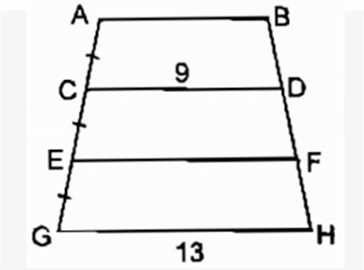
Trên hình bs.1, ta có AB // CD // EF // GH và AC = CE = EG. Biết CD = 9, GH = 13. Các độ dài AB và EF bằng:

A. 8 và 10

B.6 và 12

C. 7 và 11

D. 7 và 12

Hãy chọn phương án đúng

Xem đáp án

Chọn đáp án C. 7 và 11

Ta có : hình thang CDHG có : CD//GH và CE = EG

=> F là trung điểm của DH

=> EF là đường trung bình của hình thang CDHG => EF = (CD + HG)/2 = (9 + 13)/2 = 11

Ta có : hình thang ABFE có: AB//EF và AC = CE

=> D là trung điểm của BF

Suy ra: CD là đường trung bình của hình thang ABFE

=> CD = (AB + EF)/2 => AB= 2CD - EF => AB = 2.9 - 11 = 7

Câu 15:

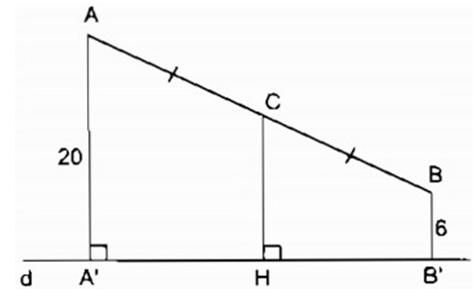
Cho đường thẳng d và hai điểm A, B có khoảng cách đến đường thẳng d theo thứ tự là 20cm và 6cm. Gọi C là trung điểm của AB. Tính khoảng cách từ C đến đường thẳng d.

Xem đáp án

Trường hợp A và B nằm trên một nửa mặt phẳng bờ chứa đường thẳng d.

Gọi A', B' là chân đường vuông góc kẻ từ A và B đến d

AA' ⊥ d; BB' ⊥ d ⇒ AA' // BB'

Tứ giác ABB'A' là hình thang. Kẻ CH ⊥ d

⇒ CH // AA' // BB' nên CH là đường trung bình của hình thang ABB'A'

⇒CH = (AA'+BB')/2 = (20 + 6)/2 = 13 (cm)

Câu 16:

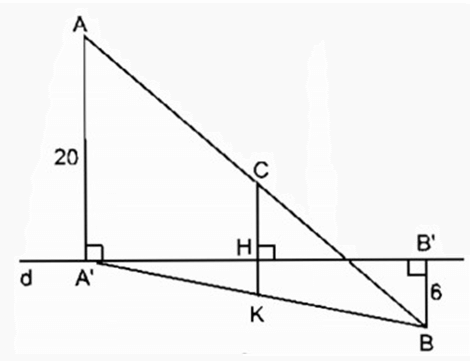
Cho đường thẳng d và hai điểm A, B có khoảng cách đến đường thẳng d theo thứ tự là 20cm và 6cm. Gọi C là trung điểm của AB. Tính khoảng cách từ C đến đường thẳng d.

Xem đáp án

Trường hợp A và B nằm trên hai nửa mặt phẳng đối bờ chứa đường thẳng d

Kẻ CH ⊥ d cắt A'B tại K

⇒ CH // AA' // BB'

Trong $∆$ AA'B ta có: AC = CB

Mà CK // AA' nên A'K = KB và CK là đường trung bình của tam giác AA'B

⇒CK= AA'/2 (tính chất đường trung bình của tam giác)

CK = 20/2 = 10(cm)

Trong $∆$ A'BB' có A'K = KB và KH // BB'

Nên KH là đường trung bình của $∆$ A'BB'

⇒ KH = BB'/2 (tính chất đường trung bình của tam giác)

⇒ KH = 6/2 =3 (cm)

CH = CK – KH = 10 – 3 = 7(cm)

Câu 17:

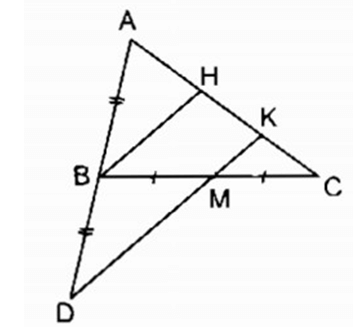
Cho tam giác ABC. Gọi M là trung điểm của BC. Trên tia đối của tia BA lấy điểm D sao cho BD = AB. Gọi K là giao điểm của DM và AC. Chứng minh rằng AK = 2KC.

Xem đáp án

Gọi H là trung điểm của AK

Trong $∆$ ADK ta có BH là đường trung bình của $∆$ ADK.

⇒ BH // DK (tính chất đường trung bình của tam giác)

Hay BH // MK

Trong $∆$ BCH ta có M là trung điểm của BC

MK // BH

⇒ CK = HK

AK = AH + HK = 2HK

Suy ra: AK = 2 KC ( vì HK =KC)

CHỌN BỘ SÁCH BẠN MUỐN XEM

Giải Sách Bài Tập Toán 8 Tập 1

Bài 4: Toán 8 Đường trung bình của tam giác, của hình thang

Danh sách câu hỏi

Bài thi liên quan