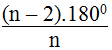17 câu hỏi trắc nghiệm thuộc Bài 1: Toán 8 Đa giác. Đa giác đều (tập 1)

Giải Sách Bài Tập Toán 8 Tập 1

Đề số 1
Đề số 2
Đề số 3
Đề số 4
Đề số 5
Đề số 6
Đề số 7
Đề số 8
Đề số 9
Đề số 10
Đề số 11
Đề số 12
Đề số 13
Đề số 14
Đề số 15
Đề số 16
Đề số 17
Đề số 18
Đề số 19
Đề số 20
Đề số 21
Đề số 22
Đề số 23
Đề số 24
Đề số 25
Đề số 26
Đề số 27
Đề số 28
Đề số 29
Đề số 30
Đề số 31
Đề số 32
Đề số 33
Đề số 34
Đề số 35
Đề số 36
Đề số 37
Đề số 38
Đề số 39
Đề số 40
Đề số 41

Bài 1: Toán 8 Đa giác. Đa giác đều (tập 1)

7200 lượt thi
17 câu hỏi
30 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

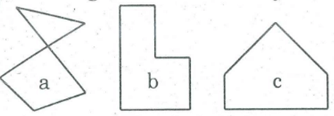
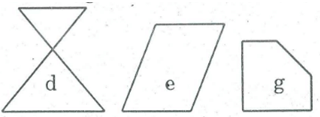
Trong các hình dưới đây hình nào là đa giác lồi? Vì sao?

Xem đáp án

Các hình c, e, g là các đa giác lồi vì đa giác nằm trên một nửa mặt phẳng với bờ chứa bất kỳ cạnh nào của đa giác.

Câu 2:

Hình vẽ bên. Hãy vẽ một đa giác lồi mà các đỉnh là một trong các điểm đã cho trong hình.

Xem đáp án

Câu 3:

Cho ví dụ về các đa giác đều mà cạnh của chúng bằng nhau.

Xem đáp án

Tam giác đều, hình vuông, ngũ giác đều, lục giác đều,…

Câu 4:

Chứng minh rằng số đo của một hình n-giác đều là $\frac{(n - 2) . 180^{0}}{n}$

Xem đáp án

Vẽ một n-giác lồi, kẻ các đường chéo xuất phát từ một đỉnh của n-giác lồi thì chia đa giác đó thành (n - 2) tam giác.

Tổng các góc của n-giác lồi bằng tổng các góc của (n - 2) tam giác bằng (n - 2).180o.

Hình n-gíác đều có n góc bằng nhau nên số đo mỗi góc bằng:

$\frac{(n - 2) . 180^{0}}{n}$

Câu 5:

Tính số đo của hình 8 cạnh đều, 10 cạnh đều, 12 cạnh đều.

Xem đáp án

Công thức tính số đo mỗi góc của đa giác đều có n cạnh:

- Đa giác đều 8 cạnh ⇒ n = 8, số đo mỗi góc là: ((8 – 2). $180^{0}$ ) / 8 = $135^{0}$

- Đa giác đều 10 cạnh ⇒ n = 10, số đo mỗi góc là: ((10 – 2). $180^{0}$ ) / 10 = $144^{0}$

- Đa giác đều 12 cạnh ⇒ n = 12, số đo mỗi góc là: ((12 – 2). $180^{0}$ ) / 12 = $150^{0}$

Câu 6:

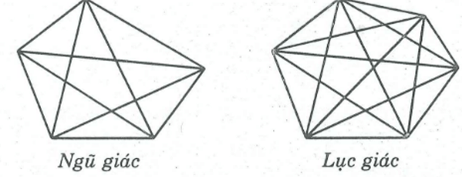
Vẽ hình và tính số đường chéo của ngũ giác, lục giác

Xem đáp án

Từ mỗi đỉnh của ngũ giác vẽ được 2 đường chéo. Ngũ giác có 5 đỉnh ta kẻ được 5.2=10 đường chéo, trong đó mỗi đường chéo được tính hai lần. Vậy ngũ giác có tất cả 5 đường chéo.

Từ mỗi đỉnh của lục giác vẽ được 3 đường chéo. Lục giác có 6 đỉnh ta kẻ được 6.3 = 18 đường chéo, trong đó mỗi đường chéo được tính hai lần. Vậy lục giác có tất cả 9 đường chéo.

Câu 7:

Chứng minh rằng hình n-giác có tất cả $\frac{n (n - 3)}{2}$ đường chéo.

Xem đáp án

Từ mỗi đỉnh của n-giác nối với các đỉnh còn lại ta được n – 1 đoạn thẳng, trong đó có 2 đoạn thẳng là cạnh của hình n-giác (hai đoạn thẳng nối với hai đỉnh kề nhau).

Vậy qua mỗi đỉnh n-giác vẽ được n-3 đường chéo. Hình n-giác có n đỉnh kẻ được n(n- 3) đường chéo, trong đó mỗi đường chéo được tính hai lần. Vậy hình n-giác có tất cả $\frac{n (n - 3)}{2}$ đường chéo.

Câu 8:

Tìm số đường chéo của hình 8 cạnh, 10 cạnh, 12 cạnh

Xem đáp án

Áp dụng công thức tính ở bài 6 chương này.

Đa giác có 8 cạnh, số đường chéo là: (8.(8 – 3)) / 2 = 20 đường chéo;

Đa giác có 10 cạnh, số đường chéo là: (10.(10 – 3)) / 2 = 35 đường chéo;

Đa giác có 12 cạnh, số đường chéo là: (12.(12 – 3)) / 2 = 54 đường chéo.

Câu 9:

Chứng minh rằng tổng các góc ngoài của một đa giác có số đo bằng $360^{0}$

Xem đáp án

Tổng số đo của góc trong và góc ngoài ở mỗi đỉnh của hình n-giác bằng $180^{0}$ . Hình n-giác có n đỉnh nên tổng số đo các góc trong và góc ngoài của đa giác bằng n. $180^{0}$ . Mặt khác, ta biết tổng các góc trong của hình n-giác bằng (n – 2). $180^{0}$

Vậy tổng số đo các góc ngoài của hình n-giác là:

n. $180^{0}$ – (n – 2). $180^{0}$ = n. $180^{0}$ – n. $180^{0}$ + 2. $180^{0}$ = $360^{0}$

Câu 10:

Đa giác nào có tổng số đo các góc trong bằng tổng số đo các góc ngoài?

Xem đáp án

Hình n-giác lồi có tổng số đo các góc trong bằng (n – 2). $180^{0}$ và tổng các góc ngoài bằng $360^{0}$

Đa giác lồi có tổng các góc trong bằng tổng các góc ngoài bằng $360^{0}$

⇒ (n – 2). $180^{0}$ = $360^{0}$ ⇒n = 4

Vậy tứ giác lồi có tổng các góc trong và góc ngoài bằng nhau.

Câu 11:

Đa giác có nhiều nhất là bao nhiêu góc nhọn?

Xem đáp án

Ta có: nếu góc của đa giác lồi là góc nhọn thì góc ngoài tương ứng là góc tù. Nếu đa giác lồi có 4 góc nhọn thì tổng các góc ngoài của đa giác lớn hơn 360o.

Vậy đa giác lồi có nhiều nhất là 3 góc nhọn.

Câu 12:

Một đa giác đều có tổng số đo tất cả các góc ngoài và một góc trong của đa giác đó bằng $468^{0}$ . Hỏi đa giác đều đó có mấy cạnh?

Xem đáp án

Tổng số đo các góc ngoài của đa giác bằng $360^{0}$

Số đo một góc trong của đa giác đều là $468^{0}$ – $360^{0}$ = $108^{0}$

Gọi n là số cạnh của đa giác đều. Ta có số đo mỗi góc của đa giác đều bằng

Suy ra: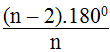= $108^{0}$ ⇒ 180.n – 360 = 108.n⇒ 72n = 360⇒ n = 5

Vậy đa giác đều cần tìm có 5 cạnh.

Câu 13:

Mỗi câu sau đây đúng hay sai ?

a. Tam giác và tứ giác không phải là đa giác

b. Hình gồm n đoạn thẳng đôi một có một điểm chung được gọi là đa giác (với n là số tự nhiên lớn hơn 2)

c. Hình gồm n đoạn thẳng (n là số tự nhiên lớn hơn 2) trong đó bất kì hai đoạn thẳng nào có một điểm chung cũng không cùng nằm trên một đường thẳng được gọi là đa giác.

d. Hình tạo bởi nhiều hình tam giác được gọi là đa giác

e. Đa giác luôn nằm trong nửa mặt phẳng cho trước được gọi là đa giác lồi

f. Đa giác luôn nằm trong nửa mặt phẳng có bờ là một đường thẳng chứa một cạnh của nó được gọi là đa giác lồi

g. Hình gồm hai đa giác lồi cho trước là một đa giác lồi.

Xem đáp án

a. Sai; b. Sai; c. Đúng; d. Sai; e. Sai; f. Sai; g. Sai

Câu 14:

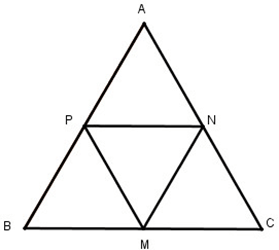
Cho tam giác đều ABC. Gọi M,N,P tương ứng là trung điểm của các cạnh BC, CA, AB. Chứng minh MNP là tam giác đều.

Xem đáp án

Ta có: M là trung điểm của BC

N là trung điểm của AC nên MN là đường trung bình của Δ ABC ⇒ MN = 1/2 AB

Ta có: P là trung điểm của AB nên MP là đường trung bình của $△$ ng bình của $△$ ABC ⇒ NP = 1/2 BC

Mà AB = BC = AC (gt) ⇒ MN = MP = NP. Vậy $△$ MNP đều

Câu 15:

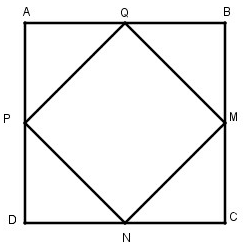
Cho hình vuông ABCD. Gọi M, N, P, Q tương ứng là trung điểm của các cạnh BC, CD, DA, AB. Chứng minh MNPQ là hình vuông (tứ giác đều)

Xem đáp án

Do ABCD là hình vuông có M, N, P, Q lần lượt là trung điểm của BC, CD, DA, AB nên: AQ = QB = BM = MC= CN = ND = DP = PA

Xét Δ APQ và Δ BQM:

AQ = BM (gt)

$∠$ A = $∠$ B = $90^{0}$

AP = BQ (gt)

Do đó: $△$ APQ = $△$ BQM (c.g.c) ⇒ PQ = QM (1)

Xét $△$ BQM và $△$ CMN:

BM = CN (gt)

$∠$ B = $∠$ C = $90^{0}$

BQ = CM (gt)

Do đó: $△$ BQM = $△$ CMN (c.g.c) ⇒ QM = MN (2)

Xét $△$ CMN và $△$ DNP:

CN = DP (gt)

$∠$ C = $∠$ D = $90^{0}$

CM = DN (gt)

Do đó: $△$ CMN = $△$ DNP (c.g.c) ⇒ MN = NP (3)

Từ (1), (2) và (3) suy ra: MN = NP = PQ = QM

nên tứ giác MNPQ là hình thoi

Vì AP = AQ nên $△$ APQ vuông cân tại A

BQ = BM nên $△$ BMQ vuông cân tại B

⇒ $∠$ (AQP) = $∠$ (BQM) = $45^{0}$

$∠$ (AQP) + $∠$ (PQM) + $∠$ (BQM) = $180^{0}$ (kề bù)

⇒ $∠$ (PQM) = $180^{0}$ - ( $∠$ (AQP) + $∠$ (BQM) )

= $180^{0}$ - ( $45^{0}$ + $45^{0}$ ) = $90^{0}$

Vậy tứ giác MNPQ là hình vuông.

Câu 16:

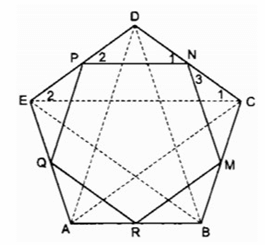
Cho ngũ giác đều ABCDE. Gọi M, N, P, Q,, R tương ứng là trung điểm của các cạnh BC, CD, DE, EA, AB. Chứng minh MNPQR là ngũ giác đều.

Xem đáp án

Xét $△$ ABC và $△$ BCD:

AB = BC (gt)

$∠$ B = $∠$ C (gt)

BC = CD (gt)

Do đó: $△$ ABC = $△$ BCD (c.g.c)

⇒ AC = BD (1)

Xét $△$ BCD và $△$ CDE:

BC = CD (gt)

$∠$ C = $∠$ D (gt)

CD = DE (gt)

Do đó: $△$ BCD = $△$ CDE (c.g.c) ⇒ BD = CE (2)

Xét $△$ CDE và $△$ DEA:

CD = DE (gt)

$∠$ D = $∠$ E (gt)

DE = EA (gt)

Do đó: $△$ CDE = $△$ DEA (c.g.c) ⇒ CE = DA (3)

Xét $△$ DEA và $△$ EAB:

DE = EA (gt)

$∠$ E = $∠$ A (gt)

EA = AB (gt)

Do đó: $△$ DEA = $△$ EAB (c.g.c) ⇒ DA = EB (4)

Từ (1), (2), (3), (4) suy ra: AC = BD = CE = DA = EB

Trong $△$ ABC ta có RM là đường trung bình

⇒ RM = 1/2 AC (tính chất đường trung bình của tam giác)

Mặt khác, ta có: Trong Δ BCD ta có MN là đường trung bình

⇒ MN = 1/2 BD (tính chất đường trung bình của tam giác)

Trong $△$ CDE ta có NP là đường trung bình

⇒ NP = 1/2 CE (tính chất đường trung bình của tam giác)

Trong $△$ DEA ta có PQ là đường trung bình

⇒ PQ = 1/2 DA (tính chất đường trung bình của tam giác)

Trong $△$ EAB ta có QR là đường trung bình

⇒ QR = 1/2 EB (tính chất đường trung bình của tam giác)

Suy ra: MN = NP = PQ = QR = RM

Ta có: $∠$ A = $∠$ B = $∠$ C = $∠$ D = $∠$ E = ((5-2 ). $180^{0}$ )/5 = $108^{0}$

$△$ DPN cân tại D

⇒ $∠$ (DPN) = $∠$ (DNP) = ( $180^{0}$ - $∠$ D )/2 = ( $180^{0}$ - $108^{0}$ )/2 = $36^{0}$

$△$ CNM cân tại C

⇒ $∠$ (CNM) = $∠$ (CMN) = ( $180^{0}$ - $∠$ D )/2 = ( $180^{0}$ - $108^{0}$ )/2 = $36^{0}$

$∠$ (ADN) + $∠$ (PNM) + $∠$ (CNM) = $180^{0}$

⇒ $∠$ (PNM) = $180^{0}$ - ( $∠$ (ADN) + $∠$ (CNM) )

= $180^{0}$ - ( $36^{0}$ – $36^{0}$ ) = $108^{0}$

$△$ BMR cân tại B

⇒ $∠$ (BMR) = $∠$ (BRM) = ( $180^{0}$ - $∠$ B )/2 = ( $180^{0}$ - $108^{0}$ )/2 = $36^{0}$

$∠$ (CMN) + $∠$ (BRM) + $∠$ (BMR) = $180^{0}$

⇒ $∠$ (NMR) = $180^{0}$ - ( $∠$ (CMN) + $∠$ (BMR) )

= $180^{0}$ - ( $36^{0}$ – $36^{0}$ ) = $108^{0}$

$△$ ARQ cân tại A

⇒ $∠$ (ARQ) = $∠$ (AQR) = ( $180^{0}$ - $∠$ A )/2 = ( $180^{0}$ - $108^{0}$ )/2 = $36^{0}$

$∠$ (BRM) + $∠$ (MRQ) + $∠$ (ARQ) = $180^{0}$

⇒ $∠$ (MRQ) = $180^{0}$ - ( $∠$ (BRM) + $∠$ (ARQ) )

= $180^{0}$ - ( $36^{0}$ – $36^{0}$ ) = $108^{0}$

$△$ QEP cân tại E

⇒ $∠$ (EQP) = $∠$ (EPQ) = ( $180^{0}$ - $∠$ E )/2 = ( $180^{0}$ - $108^{0}$ )/2 = $36^{0}$

$∠$ (AQR) + $∠$ (RQP) + $∠$ (EQP) = $180^{0}$

⇒ $∠$ (RQP) = $180^{0}$ - ( $∠$ (AQR) + $∠$ (EQP) )

= $180^{0}$ - ( $36^{0}$ – $36^{0}$ ) = $108^{0}$

$∠$ (EQP) + $∠$ (QPN) + $∠$ (DPN) = $180^{0}$

⇒ $∠$ (QPN) = $180^{0}$ - ( $∠$ (EPQ) + $∠$ (DPN) )

= $180^{0}$ - ( $36^{0}$ – $36^{0}$ ) = $108^{0}$

Suy ra : $∠$ (PNM) = $∠$ (NMR) = $∠$ (MRQ) = $∠$ (RQP) = $∠$ (QPN)

Vậy MNPQR là ngũ giác đều.

Câu 17:

Cho hình vuông ABCD có AB = 3cm

Trên tia đối của tia BA lấy điểm K sao cho BK = 1cm

Trên tia đối của tia CB lấy điểm L sao cho CL = 1cm

Trên tia đối của tia DC lấy điểm M sao cho MD = 1cm

Trên tia đối của tia AD lấy điểm N sao cho NA = 1cm

Chứng minh KLMN là hình vuông

Xem đáp án

Xét $△$ ANK và $△$ BKL :

AN = BK (gt)

$∠$ A = $∠$ B = $90^{0}$

AK = BL (vì AB = BC, BK = CL)

Do đó $△$ ANK = $△$ BKL (c.g.c)

⇒ NK = KL (1)

Xét $△$ BKL và $△$ CLM:

BK = CL (gt)

$∠$ B = $∠$ C = $90^{0}$

BL = CM (vì BC = CD, CL = DM)

Do đó: $△$ BKL = $△$ CLM (c.g.c)

⇒ KL = LM (2)

Xét $△$ CLM và $△$ DMN :

CL = DM (gt)

$∠$ C = $∠$ D = $90^{0}$

CM = DN (vì CD = DA, DM = AN)

Do đó: $△$ CLM = $△$ DMN (c.g.c)

⇒ LM = MN (3)

Từ (1), (2) và (3) ⇒ NK = KL = LM = MN

Tứ giác MNKL là hình thoi

$△$ ANK = $△$ BKL ⇒ $∠$ (ANK) = $∠$ (BKL)

Trong tam giác ANK có A là góc vuông ⇒ $∠$ (ANK) + $∠$ (AKN) = $90^{0}$

⇒ $∠$ (BKL) + $∠$ (AKN) = $90^{0}$ hay $∠$ (NKL) = $90^{0}$

Vậy tứ giác MNKL là hình vuông.

Bắt đầu thi ngay

CHỌN BỘ SÁCH BẠN MUỐN XEM

Giải Sách Bài Tập Toán 8 Tập 1

Bài 1: Toán 8 Đa giác. Đa giác đều (tập 1)

Danh sách câu hỏi

Bài thi liên quan