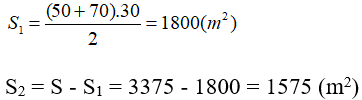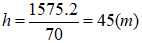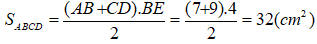16 câu hỏi trắc nghiệm thuộc Bài 4: Toán 8 Diện tích hình thang (tập 1)

Giải Sách Bài Tập Toán 8 Tập 1

Đề số 1
Đề số 2
Đề số 3
Đề số 4
Đề số 5
Đề số 6
Đề số 7
Đề số 8
Đề số 9
Đề số 10
Đề số 11
Đề số 12
Đề số 13
Đề số 14
Đề số 15
Đề số 16
Đề số 17
Đề số 18
Đề số 19
Đề số 20
Đề số 21
Đề số 22
Đề số 23
Đề số 24
Đề số 25
Đề số 26
Đề số 27
Đề số 28
Đề số 29
Đề số 30
Đề số 31
Đề số 32
Đề số 33
Đề số 34
Đề số 35
Đề số 36
Đề số 37
Đề số 38
Đề số 39
Đề số 40
Đề số 41

Bài 4: Toán 8 Diện tích hình thang (tập 1)

7177 lượt thi
16 câu hỏi
30 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

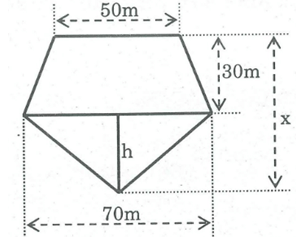
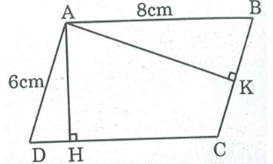
Tìm x, biết đa giác ở hình vẽ có diện tích bằng 3375 $m^{2}$

Xem đáp án

Hình đa giác đã cho gồm một hình thang và một hình tam giác.

Diện tích phần hình thang là $S_{1}$ , tam giác là $S_{2}$ , ta có:

Tam giác có chiều cao h ứng với cạnh đáy là 70 m

Diện tích tam giác là:

Suy ra: Chiều cao h của tam giác là:

Vậy x = 45 + 30 = 75 (m)

Câu 2:

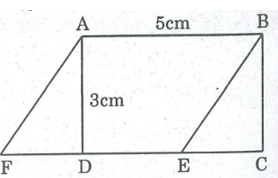
Cho hình chữ nhật ABCD có cạnh AB = 5cm, BC = 3cm. Vẽ hình bình hành ABEF có cạnh AB = 5cm và diện tích bằng diện tích hình chữ nhật. Vẽ được bao nhiêu hình như vậy ?

Xem đáp án

Trên cạnh CD ta lấy 1 điểm E bất kỳ (E khác C và D). Nối BE. Từ A kẻ đường thẳng song song với BE cắt đường thẳng CD tại F.

Tứ giác ABEF có các cạnh đối song song với nhau nên ABEF là hình bình hành

$S_{A B E F}$ = AD.EF = AD. AB ( AB = EF vì ABEF là hình bình hành)

Diện tích hình chữ nhật: $S_{A B C D}$ = AB.AD

⇒ $S_{A B C D}$ = $S_{A B E F}$

Có thể vẽ được vô số hình như vậy.

Câu 3:

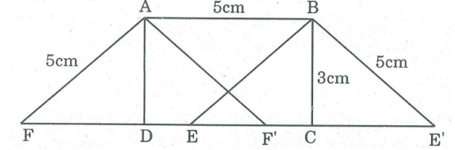
Cho hình chữ nhật ABCD có cạnh AB = 5cm, BC=3cm. Vẽ hình bình hành ABEF có cạnh AB = 5cm, BE = 5cm và có diện tích bằng diện tích của hình chữ nhật ABCD. Vẽ được mấy hình như vậy?

Xem đáp án

Vẽ cung tròn tâm B bán kính 5cm cắt CD tại 2 điểm E và E'.

Nối BE, từ A kẻ đường thẳng song song với BE cắt CD tại F.

Nối BE', từ A kẻ đường thẳng song song với BE' cắt CD tại F'.

Ta có hình bình hành ABEF và hình bình hành ABE'F' có cạnh AB = 5cm, BE = 5cm, BE' = 5cm có diện tích bằng điện tích hình chữ nhật ABCD.

Có thể vẽ được hai hình như vậy.

Câu 4:

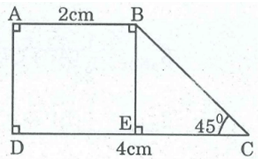
Tính diện tích của hình thang vuông, biết hai đáy có độ dài là 2cm, 4cm, góc tạo bởi một cạnh bên và đáy lớn có số đo bằng $45^{0}$

Xem đáp án

Giả sử hình thang vuông ABCD có:

$∠$ A = $∠$ D = $90^{0}$ ; $∠$ C = $45^{0}$

Kẻ BE ⊥ CD

Tam giác vuông BEC có $∠$ (BEC) = $90^{0}$ cân tại E ⇒ BE = EC

Hình thang ABCD có hai cạnh bên AD // BE (vì cùng vuông góc với DC) ⇒ DE = AB = 2cm

EC = DC – DE = 4 – 2 = 2 (cm) ⇒ BE = 2cm ( vì tam giác BEC là tam giác vuông cân).

SABCD = 1/2 .BE(AB+ CD) = 1/2 .2.(2 + 4) = 6 ( $c m^{2}$ )

Câu 5:

Tính diện tích hình thang, biết các dây có độ dài là 7cm và 9cm, một trong các cạnh bên dài 8cm và tạo với đây một góc có số đo bằng $30^{0}$

Xem đáp án

Giả sử hình thang ABCD có đáy AB = 7cm và CD = 9cm , cạnh bên BC = 8cm, $∠$ C = $30^{0}$

Kẻ BE ⊥ CD. Tam giác vuông GBE có $∠$ E = $90^{0}$ , $∠$ C = $30^{0}$

Suy ra $∠$ (CBE) = $60^{0}$ nên nó là một nửa tam giác đều có cạnh là CB.

⇒ BE = 1/2 CB = 4 (cm)

Vậy

Câu 6:

Chứng minh rằng mọi đường thẳng đi qua trung điểm của đường trung bình của hình thang và cắt hai dây hình thang sẽ chia hình thang đó thành hai hình thang có diện tích bằng nhau.

Xem đáp án

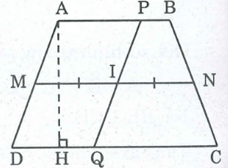
Giả sử hình thang ABCD có AB // CD, đường trung bình là MN. Gọi I là trung điểm của MN, đường thẳng bất kỳ đi qua I cắt AB tại P và CD tại Q.

Ta có hai hình thang APQD và BPQC có cùng đường cao.

MI là đường trung bình của hình thang APQD.

Suy ra: MI = 1/2 (AP + QD)

IN là đường trung bình của hình thang BPQC.

Suy ra: IN = 1/2 (BP + QC)

$S_{A P Q D}$ = 1/2 (AP + QD).AH = MI.AH (1)

$S_{B P Q C}$ = 1/2 (BP + QC).AH = IN.AH (2).

IM = IN (gt) (3)

Từ (1), (2) và (3) suy ra: $S_{A P Q D} = S_{B P Q C}$ , các giá trị này không phụ thuộc vào vị trí của P và Q.

Câu 7:

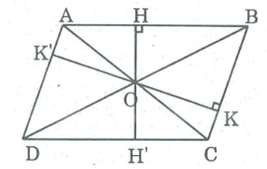
Diện tích hình bình hành bằng 24 $c m^{2}$ . Khoảng cách từ giao điểm hai đường chéo đến các cạnh hình bình hành bằng 2cm và 3cm. Tính chu vi của hình bình hành.

Xem đáp án

Gọi O là giao điểm hai đường chéo của hình bình hành ABCD, khoảng cách từ O đến cạnh AB là OH = 2cm , đến cạnh BC là OK = 3cm

* Kéo dài OH cắt cạnh CD tại H'.

Ta có OH ⊥ BC

⇒ OH' ⊥ CD và OH' = 2cm

Suy ra HH' bằng đường cao của hình bình hành.

$S_{A B C D}$ = HH'.AB ⇒

* Kéo dài OK cắt AD tại K'.

Ta có: OK ⊥ BC ⇒ OK' ⊥ CD và OK' = 3 (cm)

Suy ra KK' là đường cao của hình bình hành.

$S_{A B C D}$ = KK'.AB ⇒

Chu vi của hình bình hành ABCD là (6 + 4).2 = 20 (cm).

Câu 8:

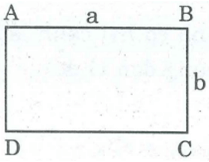
Một hình chữ nhật có các kích thước a và b. Một hình bình hành cũng có hai cạnh là a và b. Tính góc nhọn của hình bình hành nếu diện tích của nó bằng một nửa diện tích hình chữ nhật (a và b có cùng đơn vị đo).

Xem đáp án

* Xét hình chữ nhật ABCD có chiều dài AB = a, chiều rộng AD = b.

Ta có: $S_{A B C D}$ = ab.

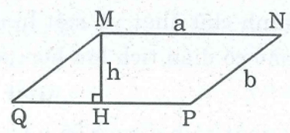
* Hình bình hành MNPQ có góc M là góc tù, MN = a, cạnh MQ = b

Kẻ đường cao MH. Ta có: $S_{M N P Q}$ = MH.a

Theo bài ra, ta có: MH.a = 1/2 ab

Suy ra: MH = 1/2 b hay MH = MQ/2

Tam giác MHQ vuông tại H và MH = MQ/2

Cạnh đối diện góc nhọn bằng một nửa cạnh huyền nên $∠$ (MQH) = $30^{0}$

Vậy góc nhọn của hình bình hành bằng $30^{0}$ .

Câu 9:

Hai cạnh của một hình hình hành có độ dài là 6cm và 8cm. Một trong các đường cao có độ dài là 5cm. Tính độ dài đường cao thứ hai. Hỏi bài toán có mấy đáp số.

Xem đáp án

Giả sử hình bình hành ABCD cói AB = 8cm, AD = 6cm.

Kẻ AH ⊥ CD, AK ⊥ BC.Ta có 5 < 6, 5 < 8

Đường cao là cạnh góc vuông nhỏ hơn cạnh huyền thỏa mãn có hai trường hợp:

*Trường hợp 1: AK = 5cm

Ta có: $S_{A B C D}$ = AK.BC = 5.6 = 30 ( $c m^{2}$ )

$S_{A B C D}$ = AH.AD = 8.AH

Suy ra: 8.AH = 30 ⇒ AH = 30/8 = 15/4 (cm)

*Trường hợp 2: AH = 5cm

Ta có: $S_{A B C D}$ = AH.CD= 5.8 = 40 ( $c m^{2}$ )

$S_{A B C D}$ = AK.BC = 6.AH

Suy ra: 6.AK = 40 ⇒ AK = 40/6 = 20/3 (cm)

Vậy đường cao thứ hai có độ dài là 15/4 cm hoặc 20/3 cm

Bài toán có hai đáp số.

Câu 10:

Một hình chữ nhật và một hình bình hành có hai cạnh là a và b. Hỏi hình nào có diện tích lớn hơn (a vàb có cùng đơn vị do).

Xem đáp án

Hình chữ nhật có hai cạnh là a và b nên $S_{c h ữ n h ậ t}$ = ab

Hình bình hành có hai cạnh là a và b. Kẻ đường cao ứng với cạnh bằng ạ thì h < b (vì cạnh góc vuông nhỏ hơn cạnh huyền).

Nếu kẻ đường cao ứng với cạnh bằng b thì h < a (cạnh góc vuông nhỏ hơn cạnh huyền).

Diện tích của hình bình hành là: $S_{h ì n h b ì n h h à n h}$ = a.h = b.h'

Mà h < b và h' < a nên $S_{h ì n h b ì n h h à n h}$ < $S_{c h ữ n h ậ t}$

Câu 11:

Tính diện tích của hình được cho trong mỗi trường hợp sau: Hình thang ABCD, đáy lớn AB = 10cm, đáy nhỏ CD = 6cm và đường cao DE = 5cm

Xem đáp án

Áp dụng công thức tính diện tích hình thang.

S = (a+b)/2.h = (10+6)/2. 5 = 40( $c m^{2}$ )

Câu 12:

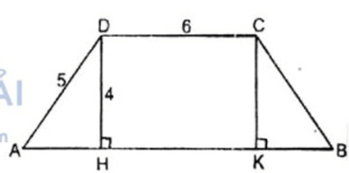
Tính diện tích của hình được cho trong mỗi trường hợp sau: Hình thang cân ABCD, đáy nhỏ CD = 6cm, đường cao DH = 4cm và cạnh bên AD = 5cm.

Xem đáp án

Xét hình thang cân ABCD có AB // CD

Đáy nhỏ CD = 6cm, cạnh bên AD = 5cm

Đường cao DH = 4cm. Kẻ CK ⊥ AB

Ta có tứ giác CDHK là hình chữ nhật

HK = CD = 6cm

$△$ AHD vuông tại H. Theo định lý Pi-ta-go ta có: $A D^{2} = A H^{2} + D H^{2}$

⇒ $A H^{2} = A D^{2} - D H^{2}$ = $5^{2} - 4^{2}$ = 25 – 16 = 9 ⇒ AH = 3cm

Xét hai tam giác vuông DHA và CKB :

$∠$ (DHA)= $∠$ (CKB)= $90^{0}$

AD = BC (tính chất hình thang cân)

$∠$ A = $∠$ B(gt)

Do đó: $△$ DHA = $△$ CKB (cạnh huyền, góc nhọn)

⇒ KB = AH = 3 (cm)

AB = AH + HK + KB = 3 + 6 + 3 = 12 (cm)

$S_{A B C D}$ = (AB + CD) / 2. DH = (12 + 6) / 2. 4 = 36( $c m^{2}$ )

Câu 13:

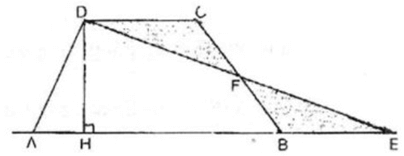
Cho hình thang ABCD có đáy nhỏ CD và đáy lớn AB. Hãy vẽ tam giác ADE mà diện tích của nó bằng diện tích hình thang đã cho. Từ đó suy ra cách tính diện tích hình thang dựa vào độ dài hai cạnh đáy và độ dài đường cao của hình thang.

Xem đáp án

Gọi F là trung điểm của cạnh bên BC. Cắt hình thang theo đường DF đưa ghép về như hình vẽ bên, điểm C trung với điểm B, D trùng với E.

Vì AB // CD ⇒ $∠$ (ABC) = $180^{0}$ ⇒ A, B, E thẳng hàng

$∠$ (ABF) + $∠$ (DFC) = $180^{0}$

⇒ D, F, E thẳng hàng

$△$ DFC = $△$ EFB (g.c.g)

$S_{D F C} = S_{E F B}$

Suy ra: $S_{A B C D} = S_{A D E}$

$△$ DFC = $△$ EFB⇒ DC = BE

AE = AB + BE = AB + DC

$S_{A D E}$ = 1/2 DH. AE = 1/2 DH. (AB + CD)

Vậy : $S_{A B C D}$ = 1/2 DH. (AB + CD)

Câu 14:

Cho hình thang ABCD có đáy nhỏ CD và đáy lớn AB. Hãy chia hình thang đã cho thành hai phần có diện tích bằng nhau bằng một đường thẳng đi qua đỉnh D của nó.

Xem đáp án

Dựa trên hình vẽ câu a ta chọn điểm K là trung điểm AE.

Câu 15:

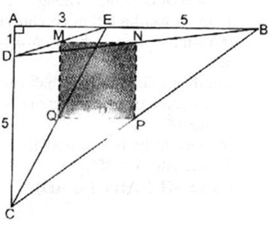
Cho hình bình hành ABCD có diện tích S. Trên cạnh BC lấy hai điểm M, N sao cho BM = MN = NC = 1/3 BC. Tính diện tích của tứ giác ABMD theo S

Xem đáp án

$△$ DMC có CM = 2/3BC

Hình bình hành ABCD và ΔDMC có chung đường cao kẻ từ đỉnh D đến BC.

Gọi độ dài đường cao là h, BC = a

Ta có diện tích hình bình hành ABCD là S = a h

$S_{D M C}$ = 1/2 h. 2/3 a = 1/3 ah = 1/3 S

$S_{A B M D}$ = $S_{A B C D}$ - $S_{D M C}$ = s - 1/3 S = 2/3 S

Câu 16:

Cho hình bình hành ABCD có diện tích S. Trên cạnh BC lấy hai điểm M, N sao cho BM = MN = NC = 1/3 BC. Từ điểm N kẻ NT song song với AB (T thuộc AC). Tính diện tích của tứ giác ABNT theo S

Xem đáp án

$S_{A B C}$ = 1/3 $S_{A B C D}$ = S/2

CN = 1/3 BC , NT // AB.

Theo tính chất đường thẳng song song cách đều ⇒ CT = 1/3 AC

$△$ ABC và $△$ BTC có chung chiều cao kẻ từ đỉnh B, đáy CT = 1/3 AC

⇒ $S_{B T C}$ = 1/3 $S_{A B C}$ = 1/3 . S/2 = S/6

$△$ BTC và $△$ TNC có chung chiều cao kẻ từ đỉnh T, cạnh đáy CN = 1/3 CB

⇒ $S_{T N C}$ = 1/3 $S_{B T C}$ = 1/3 . S/6 = S/18

$S_{A B N T}$ = $S_{A B C}$ - $S_{T N C}$ = S/2 - S/18 = 9S/18 - S/18 = 4S/9

Bắt đầu thi ngay

CHỌN BỘ SÁCH BẠN MUỐN XEM

Giải Sách Bài Tập Toán 8 Tập 1

Bài 4: Toán 8 Diện tích hình thang (tập 1)

Danh sách câu hỏi

Bài thi liên quan