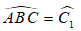16 câu hỏi trắc nghiệm thuộc Bài 2: Toán 8 Hình thang

Giải Sách Bài Tập Toán 8 Tập 1

Đề số 1
Đề số 2
Đề số 3
Đề số 4
Đề số 5
Đề số 6
Đề số 7
Đề số 8
Đề số 9
Đề số 10
Đề số 11
Đề số 12
Đề số 13
Đề số 14
Đề số 15
Đề số 16
Đề số 17
Đề số 18
Đề số 19
Đề số 20
Đề số 21
Đề số 22
Đề số 23
Đề số 24
Đề số 25
Đề số 26
Đề số 27
Đề số 28
Đề số 29
Đề số 30
Đề số 31
Đề số 32
Đề số 33
Đề số 34
Đề số 35
Đề số 36
Đề số 37
Đề số 38
Đề số 39
Đề số 40
Đề số 41

Bài 2: Toán 8 Hình thang

7174 lượt thi
16 câu hỏi
30 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

Tính các góc của hình thang ABCD (AB // CD), biết rằng A = 3D, B - C = $30^{0}$

Xem đáp án

Ta có: hình thang ABCD có AB // CD ⇒ $∠$ A + $∠$ D = $180^{0}$ (hai góc trong cùng phía)

Ta có: $∠$ A = 3 $∠$ D (gt)

⇒ 3 $∠$ D + $∠$ D = $180^{0}$ ⇒ 4 $∠$ D = $180^{0}$ ⇒ $∠$ D = $45^{0}$ ⇒ $∠$ A = 3. $45^{0}$ = $135^{0}$

$∠$ B + $∠$ C = $180^{0}$ (hai góc trong cùng phía)

$∠$ B - $∠$ C = $30^{0}$ (gt)

⇒ 2 $∠$ B = $180^{0}$ + $30^{0}$ = $210^{0}$ ⇒ $∠$ B = $105^{0}$

$∠$ C = $∠$ B - $30^{0}$ = $105^{0}$ – $30^{0}$ = $75^{0}$

Câu 2:

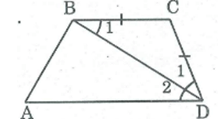
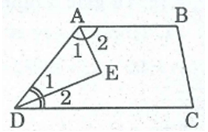
Tứ giác ABCD có BC = CD và DB là tia phân giác của góc D. chứng minh rằng ABCD là hình thang

Xem đáp án

ΔBCD có BC = CD (gt) nên ΔBCD cân tại C.

⇒ $∠ B_{1}$ = $∠ D_{1}$ (tính chất tam giác cân)

Mà $∠ D_{1}$ = $∠ D_{2}$ ( Vì DB là tia phân giác của góc D)

Suy ra: $∠ B_{1}$ = $∠ D_{2}$

Do đó: BC // AD (vì có cặp góc ở vị trí so le trong bằng nhau)

Vậy ABCD là hình thang.

Câu 3:

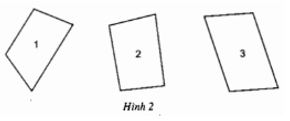
Xem các hình dưới và cho biết:

a. Tứ giác nào chỉ có một cặp cạnh song song?

b. Tứ giác nào có hai cặp cạnh song song?

c. Tứ giác nào là hình thang.

Xem đáp án

a. Tứ giác 1 có một cặp cạnh song song.

b. Tứ giác 3 có hai cặp cạnh song song.

c. Tứ giác 1 và 3 là hình thang.

Câu 4:

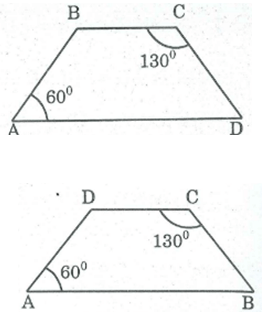
Tính các góc B và D của hình thang ABCD, biết rằng: $∠$ A = $60^{0}$ , $∠$ C = $130^{0}$

Xem đáp án

Trong hình thang ABCD, ta có A và C là hai góc đối nhau.

- Trường hợp A và B là 2 góc kề với cạnh bên.

⇒ BC // AD

$∠$ A + $∠$ B = $180^{0}$ (hai góc trong cùng phía bù nhau)

⇒ $∠$ B = $180^{0}$ - $∠$ A = $180^{0}$ – $60^{0}$ = $120^{0}$

$∠$ C + $∠$ D = $180^{0}$ (hai góc trong cùng phía bù nhau)

⇒ $∠$ D = $180^{0}$ - $∠$ C = $180^{0}$ – $130^{0} = 50^{0}$

- Trường hợp A và D là 2 góc kề với cạnh bên.

⇒ AB // CD

$∠$ A + $∠$ D = $180^{0}$ (hai góc trong cùng phía bù nhau)

⇒ $∠$ D = $180^{0}$ - $∠$ A = $180^{0}$ – $60^{0} = 120^{0}$

$∠$ C + $∠$ B = $180^{0}$ (hai góc trong cùng phía bù nhau)

⇒ $∠$ B = $180^{0}$ - $∠$ C = $180^{0}$ – $130^{0} = 50^{0}$

Câu 5:

Chứng minh rằng trong hình thang có nhiều nhất là hai góc tù, có nhiều nhất là hai góc nhọn.

Xem đáp án

Xét hình thang ABCD có AB //CD.

Ta có:

* $∠$ A và $∠$ D là hai góc kề với cạnh bên

⇒ $∠$ A + $∠$ D = $180^{0}$ (2 góc trong cùng phía) nên trong hai góc đó có nhiều nhất 1 góc nhọn và có nhiều nhất là 1 góc tù.

* $∠$ B và $∠$ C là hai góc kề với cạnh bên

⇒ $∠$ B + $∠$ C = $180^{0}$ (2 góc trong cùng phía) nên trong hai góc đó có nhiều nhất 1 góc nhọn và có nhiều nhất là 1 góc tù.

Vậy trong bốn góc là A, B, C, D có nhiều nhất là hai góc tù và có nhiều nhất là hai góc nhọn.

Câu 6:

Chứng minh rằng trong hình thang các tia phân giác của hai góc kề với một cạnh bên vuông góc với nhau.

Xem đáp án

Giả sử hình thang ABCD có AB // CD

* Ta có: $∠ A_{1}$ = $∠ A_{2}$ = 1/2 $∠$ A (vì AE là tia phân giác của góc A)

$∠ D_{1}$ = $∠ D_{2}$ = 1/2 $∠$ D ( Vì DE là tia phân giác của góc D)

Mà $∠$ A + $∠$ D = $180^{0}$ (2 góc trong cùng phía bù nhau)

Suy ra: $∠ A_{1}$ + $∠ D_{1}$ = 1/2 ( $∠$ A + $∠$ D) = $90^{0}$

* Trong ΔAED, ta có:

$∠$ (AED) + $∠ A_{1}$ + $∠ D_{1}$ = $180^{0}$ (tổng 3 góc trong tam giác)

⇒ $∠$ (AED) = $180^{0}$ – ( $∠ A_{1}$ + $∠ D_{1}$ ) = $180^{0}$ - $90^{0}$ = $90^{0}$

Vậy AE ⊥ DE.

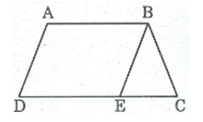
Câu 7:

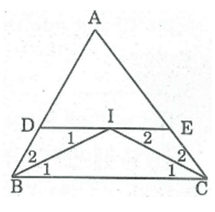
Cho tam giác ABC, các tia phân giác của các góc B và C cắt nhau ở I. Qua I kẻ đường thẳng song song với BC cắt các cạnh AB và AC ở D và E. Tìm các hình thang trong hình vẽ.

Xem đáp án

Đường thẳng đi qua I song song với BC cắt AB tại D và AC tại E, ta có các hình thang sau: BDEC, BDIC, BIEC

Câu 8:

Cho tam giác ABC, các tia phân giác của các góc B và C cắt nhau ở I. Qua I kẻ đường thẳng song song với BC cắt các cạnh AB và AC ở D và E. Chứng minh rằng hình thang BDEC có một đáy bằng tổng hai cạnh bên.

Xem đáp án

DE // BC (theo cách vẽ)

⇒ $∠ I_{1}$ = $∠ B_{1}$ (hai góc so le trong)

Mà $∠ B_{1}$ = $∠ B_{2}$ (gt)

Suy ra: $∠ I_{1}$ = $∠ B_{2}$

Do đó: $∆$ BDI cân tại D ⇒ DI = DB (1)

Ta có: $∠ I_{2}$ = $∠ C_{1}$ (so le trong)

$∠ C_{1}$ = $∠ C_{2}$ (gt)

Suy ra: $∠ I_{2}$ = $∠ C_{2}$ do đó: $∆$ CEI cân tại E

⇒ IE = EC (2)

DE = DI + IE (3)

Từ (1), (2), (3) suy ra: DE = BD + CE

Câu 9:

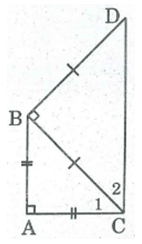
Cho tam giác ABC vuông cân tại A. Ở phía ngoài tam giác ABC, vẽ tam giác BCD vuông cân tại B. Tứ giác ABCD là hình gì? Vì sao?

Xem đáp án

Vì ΔABC vuông cân tại A nên

Lại có: 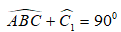( tính chất tam giác vuông).

Suy ra: $∠ C_{1}$ = $45^{0}$

Vì $∆$ BCD vuông cân tại B nên

Lại có: ( tính chất tam giác vuông).

Suy ra: $∠ C_{2}$ = $45^{0}$

$∠$ (ACD) = $∠ C_{1}$ + $∠ C_{2}$ = $45^{0}$ + $45^{0}$ = $90^{0}$

⇒ AC ⊥ CD

Mà AC ⊥ AB (gt)

Suy ra: AB //CD

Vậy tứ giác ABCD là hình thang vuông.

Câu 10:

Hình thang vuông ABCD có $∠$ A = $∠$ D = $90^{0}$ , AB = AD = 2cm, DC = 4cm. Tính các góc của hình thang.

Xem đáp án

Kẻ BH ⊥ CD

Ta có: AD ⊥ CD ( Vì ABCD là hình thang vuông có $∠$ A = $∠$ D = $90^{0}$ )

Suy ra: BH // AD

Hình thang ABHD có hai cạnh bên song song nên HD = AB và BH = AD

AB = AD = 2cm (gt)

⇒ BH = HD = 2cm

CH = CD – HD = 4 – 2 = 2 (cm)

Suy ra: $∆$ BHC vuông cân tại H

⇒ $∠$ C = $45^{0}$

$∠$ B + $∠$ C = $180^{0}$ (2 góc trong cùng phía bù nhau) ⇒ $∠$ B = $180^{0}$ – $45^{0}$ = $135^{0}$

Câu 11:

Chứng minh rằng tổng hai cạnh bên của hình thang lớn hơn hiệu của hai đáy.

Xem đáp án

Giả sử hình thang ABCD có AB // CD

Từ B kẻ đường thẳng song song với AD cắt CD tại E.

Hình thang ABED có hai cạnh bên song song nên AB = ED và AD = BE

Ta có: CD – AB = CD – ED = EC (1)

Trong $∆$ BEC ta có:

BE + BC > EC (bất đẳng thức tam giác)

Mà BE = AD

Suy ra: AD + BC > EC (2)

Từ (1) và (2) suy ra: AD + BC > CD – AB

Câu 12:

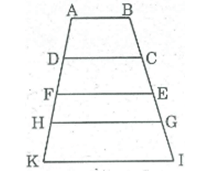
Trên hình vẽ dưới có bao nhiêu hình thang

Xem đáp án

Trên hình vẽ có tất cả 10 hình thang.

Đó là: ABCD, ABEF, ABGH, ABIK, DCEF, DCGH, DCIK, FEGH, FEIK, HGIK

Câu 13:

Hình thang ABCD (BC// AD) có $∠$ C = 3 $∠$ D. Khẳng định nào dưới đây là đúng ?

A. $∠$ (A ) = $45^{0}$

B. $∠$ (B ) = $45^{0}$

C. $∠$ (D ) = $45^{0}$

D. $∠$ (D ) = $60^{0}$

Xem đáp án

Chọn C. (D ) = 45o

Ta có : hình thang ABCD CÓ BC//AD

=> $∠$ (C )+ $∠$ (D )= $180^{0}$ ( hai góc trong cùng phía bù nhau)

mà $∠$ C = 3 $∠$ D nên 3 $∠$ D+ $∠$ D= $180^{0}$ => $∠$ D= $45^{0}$

Câu 14:

Hình thang ABCD (AB // CD) có $∠$ A - $∠$ D = $40^{0}$ , $∠$ A = 2 $∠$ C . Tính các góc của hình thang

Xem đáp án

Hình thang ABCD có AB // CD

⇒ có $∠$ A + $∠$ D = $180^{0}$ (hai góc trong cùng phía bù nhau)

$∠$ A - $∠$ D = $40^{0}$ (gt)

⇒ 2 $∠$ A = $220^{0}$ ⇒ $∠$ A = $110^{0}$

$∠$ D = $∠$ A - $40^{0}$ = $110^{0}$ – $40^{0}$ = $70^{0}$

$∠$ A = 2 $∠$ C (gt)

⇒ $∠$ C = $∠$ A /2 = $110^{0}$ : 2 = $55^{0}$

$∠$ B + $∠$ C = $180^{0}$ (hai góc trong cùng phía bù nhau)

⇒ $∠$ B = 180o- $∠$ C = $180^{0}$ – $55^{0}$ = $125^{0}$

Câu 15:

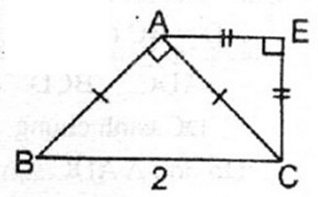
Cho tam giác ABC vuông cân tại A, BC = 2 cm. Ở phía ngoài tam giác ABC, vẽ tam giác ACE vuông cân tại E. Chứng minh rằng AECB là hình thang vuông

Xem đáp án

Tam giác ABC vuông cân tại A

⇒ $∠$ (ACB) = $45^{0}$

Tam giác EAC vuông cân tại E

⇒ $∠$ (EAC) = $45^{0}$

Suy ra: $∠$ (ACB) = $∠$ (EAC)

⇒ AE // BC (vì có cặp góc ở vị trí so le trong bằng nhau)

nên tứ giác AECB là hình thang có $∠$ E = $90^{0}$ . Vậy AECB là hình thang vuông

Câu 16:

Cho tam giác ABC vuông cân tại A, BC = 2 cm. Ở phía ngoài tam giác ABC, vẽ tam giác ACE vuông cân tại E. Tính các góc và các cạnh của hình thang AECB

Xem đáp án

$∠$ E = $∠$ (ECB) = $90^{0}$ , $∠$ B = $45^{0}$

$∠$ B + $∠$ (EAB) = $180^{0}$ (hai góc trong cùng phía bù nhau)

⇒ $∠$ (EAB) = $180^{0}$ - $∠$ B = $180^{0}$ – $45^{0}$ = $135^{0}$

Tam giác ABC vuông tại A. Theo định lí Py-ta-go ta có:

$A B^{2} + A C^{2} = B C^{2}$ mà AB = AC (gt)

⇒ $2 A B^{2} = B C^{2} = 2^{2} = 4$

$A B^{2}$ = 2 ⇒ AB= √2(cm) ⇒ AC = √2 (cm)

Tam giác AEC vuông tại E. Theo định lí Py-ta-go ta có:

$E A^{2} + E C^{2} = A C^{2}$ , mà EA = EC (gt)

⇒ $2 E A^{2} = A C^{2}$ = 2

$E A^{2}$ = 1

⇒ EA = 1(cm) ⇒ EC = 1(cm)

Bắt đầu thi ngay

CHỌN BỘ SÁCH BẠN MUỐN XEM

Giải Sách Bài Tập Toán 8 Tập 1

Bài 2: Toán 8 Hình thang

Danh sách câu hỏi

Bài thi liên quan