- Đề số 1
- Đề số 2
- Đề số 3
- Đề số 4
- Đề số 5
- Đề số 6
- Đề số 7
- Đề số 8
- Đề số 9
- Đề số 10
- Đề số 11
- Đề số 12
- Đề số 13
- Đề số 14
- Đề số 15
- Đề số 16
- Đề số 17
- Đề số 18
- Đề số 19
- Đề số 20
- Đề số 21
- Đề số 22
- Đề số 23
- Đề số 24
- Đề số 25
- Đề số 26
- Đề số 27
- Đề số 28
- Đề số 29
- Đề số 30
- Đề số 31
- Đề số 32
- Đề số 33
- Đề số 34
- Đề số 35
- Đề số 36
- Đề số 37
- Đề số 38
- Đề số 39
- Đề số 40
- Đề số 41
Bài 7: Toán 8 Hình bình hành
-
7168 lượt thi
-
29 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
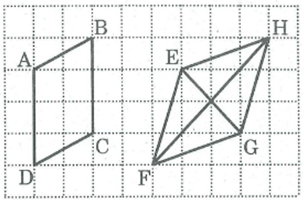
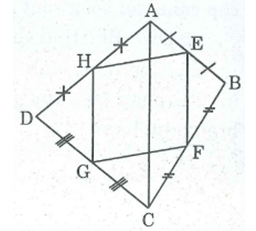
Các tứ giác ABCD, EFGH và hình vẽ bên dưới có phải là hình bình hành hay không?
 Xem đáp án
Xem đáp án
Tứ giác ABCD là hình bình hành vì có cạnh đối AD // BC và AD = BC bằng 3 cạnh ô vuông.
Tứ giác EFGH là hình bình hành vì có các cạnh đối bằng nhau.
EH = FG, EF = HG là đường chéo hình chữ nhật có cạnh 1 ô vuông và cạnh 3 ô vuông
Câu 2:
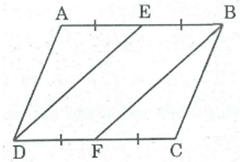
Cho hình bình hành ABCD. Gọi E là trung điểm của AB, F là trung điểm của CD. Chứng minh rằng: DE = BF
 Xem đáp án
Xem đáp án
Ta có: AB = CD (tính chất hình bình hành)
EB = 1/2 AB (gt)
FD = 1/2 CD (gt)
Suy ra: EB = FD (1)
Mà AB // CD (gt)
⇒ BE // FD (2)
Từ (1) và (2) suy ra tứ giác BEDF là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau)
⇒ DE = BF (tính chất hình bình hành)
Câu 3:
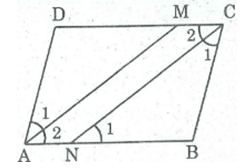
Cho hình bình hành ABCD. Tia phân giác của góc A cắt CD ở M. Tia phân giác của góc C cắt AB ở N. Chứng minh rằng AMCN là hình bình hành.
 Xem đáp án
Xem đáp án
Ta có: A = C (tính chất hình bình hành)
= 1/2 A ( Vì AM là tia phân giác của (BAD) )
= 1/2 C ( Vì CN là tia phân giác của (BCD) )
Suy ra: =
Do ABCD là hình bình hành nên AB // CD (gt)
Hay AN // CM (1)
Mà = (so le trong)
Suy ra: =
⇒ AM // CN (vì có cặp góc ở vị trí đồng vị bằng nhau) (2)
Từ (1) và (2) suy ra tứ giác AMCN là hình bình hành.
Câu 4:
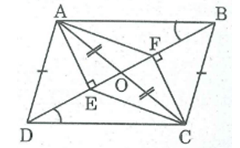
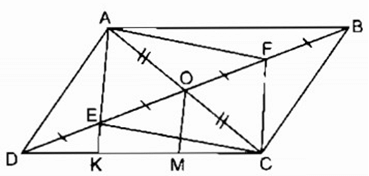
Hình bên cho ABCD là hình bình hành. Chứng minh rằng AECF là hình bình hành.
 Xem đáp án
Xem đáp án
Gọi O là'giao điểm của AC và BD, ta có:
OA = OC (tính chất hình bình hành) (1)
Xét hai tam giác vuông AEO và CFO, ta có:
(AEO) = (CFO) =
OA = OC (chứng minh trên)
(AOE) = (COF) (đối đỉnh)
Do đó AEO = CFO (cạnh huyền, góc nhọn)
⇒ OE = OF (2)
Từ (1) và (2) suy ra tứ giác AECF là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm của mỗi đường).
Câu 5:
Tứ giác ABCD có E, F, G, H theo thứ tự là trung điểm của các cạnh AB, BC, CD, DA. Tứ giác EFGH là hình gì? Vì sao?
 Xem đáp án
Xem đáp án
Nối đường chéo AC.
Trong ABC ta có:
E là trung điểm của AB (gt)
F là trung điểm của BC (gt)
Nên EF là đường trung bình của ABC
⇒EF//AC và EF = 1/2 AC
(tính chất đường trung hình tam giác) (1)
Trong ADC ta có:
H là trung điểm của AD (gt)
G là trung điểm của DC (gt)
Nên HG là đường trung bình của ADC
⇒ HG // AC và HG = 1/2 AC (tính chất đường trung bình tam giác) (2)
Từ (1) và (2) suy ra: EF // HG và EF = HG
Vậy tứ giác EFGH là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau).
Câu 6:
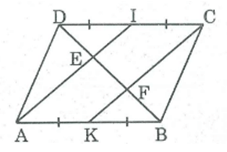
Cho hình bình hành ABCD. Gọi I, K theo thứ tự là trung điểm của CD, AB, Đường chéo BD cắt AI, CK theo thứ tự ở E, F. Chứng minh rằng DE = EF = FB
 Xem đáp án
Xem đáp án
Ta có: AB = CD (tính chất hình bình hành)
AK = 1/2 AB (gt)
CI = 1/2 CD (gt)
Suy ra: AK = CI (1)
Mặt khác: AB // CD (gt)
⇒ AK // CI (2)
Từ (1) và (2) suy ra tứ giác AKCI là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau).
⇒ AI // CK
Trong ABE, ta có:
K là trung điểm của AB (gt)
AI // CK hay KF // AE nên BF = EF (tính chất đường trung bình tam giác)
Trong DCF, ta có:
I là trung điểm của DC (gt)
AI // CK hay IE // CF nên DE = EF (tính chất đường trung bình tam giác)
Suy ra: DE = EF = FB
Câu 7:
Tính các góc của hình bình hành ABCD biết: A =
 Xem đáp án
Xem đáp án
Tứ giác ABCD là hình bình hành.
⇒ C = A = (tính chất hình bình hành)
A + B = (2 góc trong cùng phía bù nhau)
⇒ B = – =
D = B = (tính chất hình bình hành)
Câu 8:
Tính các góc của hình bình hành ABCD biết: A - B =
 Xem đáp án
Xem đáp án
Tứ giác ABCD là hình bình hành.
⇒A + B = (2 góc trong cùng phía bù nhau)
A - B = (gt)
Suy ra: 2A = ⇒ A =
C = A = (tính chất hình bình hành)
B = A – = – =
D = B = (tính chất hình bình hành)
Câu 9:
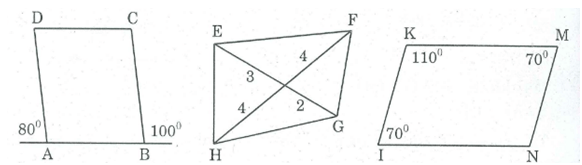
Trong các tứ giác ở hình dưới đây, hình nào là hình bình hành.
 Xem đáp án
Xem đáp án
* Tứ giác ABCD là hình bình hành vì AB // CD và AB = CD.
* Tứ giác IKMN có: I + K + N + M =
Suy ra: N = - (K + I + M) =
Ta có I = M = và K = N =
Suy ra IKMN là hình bình hành (tứ giác có các góc đối bằng nhau).
* Tứ giác EFGH không là hình bình hành vì có hai đường chéo không cắt nhau tại trung điểm mỗi đường.
Câu 10:
Chu vi hình bình hành ABCD bằng l0cm, chu vi tam giác ABD bằng 9cm. Tính độ dài BD.
 Xem đáp án
Xem đáp án
Chu vì hình bình hành ABCD bằng 10cm nên (AB + AD).2 = 10(cm)
⇒ AB + AD = 10 : 2 = 5(cm)
Chu vi của ABD bằng:
AB + AD + BD = 9(cm)
⇒ BD = 9 - (AB + AD) = 9 - 5 = 4(cm)
Câu 11:
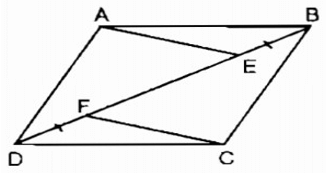
Hình bên dưới, cho ABCD là hình bình hành. Chứng minh rằng AE //CF.
 Xem đáp án
Xem đáp án
Gọi O là giao điểm của AC và BD, ta có:
OB = OE + EB và OD = OF+ FD (1)
Lại có: EB = FD (giả thiết) (2)
OB = OD ( tính chất hình bình hành). (3)
Từ (1), (2),(3) suy ra: OE = OF
Suy ra tứ giác AECF là hình bình hành (vì có 2 đường chéo cắt nhau tại trung điểm của mỗi đường)
⇒ AE // CF.
Câu 12:
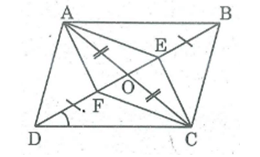
Cho hình hình hành ABCD. Gọi E, F theo thứ tự là trung điểm của AB, CD. Gọi M là giao điểm của AF và DE, N là giao điểm của BF và CE. Chứng minh rằng: EMNF là hình bình hành
 Xem đáp án
Xem đáp án
+) Ta có:
AE = 1/2 AB; CF = 1/2. CD ( vì E và F lần lượt là trung điểm của AB, CD).
Và AB = CD (tính chất hình bình hành)
Suy ra: AE = CF
+) Lại có: AB // CD ( vì ABCD là hình bình hành) nên AE //CF
Tứ giác AECF có hai cạnh đối AE, CF song song và bằng nhau nên là hình bình hành
⇒ AF //CE hay EN // FM (1)
Xét tứ giác BFDE ta có:
AB // CD (gt) hay BE // DF
BE = 1/2 AB (gt)
DF = 1/2 CD (gt)
AB = CD (tính chất hình bình hành)
Suy ra: BE = DF
Tứ giác BFDE là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau) ⇒ BF//DE hay EM // FN (2)
Từ (1) và (2) suy ra tứ giác EMFN là hình bình hành (theo định nghĩa hình bình hành)
Câu 13:
Cho hình hình hành ABCD. Gọi E, F theo thứ tự là trung điểm của AB, CD. Gọi M là giao điểm của AF và DE, N là giao điểm của BF và CE. Chứng minh rằng: Các đường thẳng AC, EF, MN đồng quy.
 Xem đáp án
Xem đáp án
Gọi O là giao điểm của AC và EF
Tứ giác AECF là hình bình hành ⇒ OE = OF
Tứ giác EMFN là hình bình hành nên hai đường chéo cắt nhau tại trung điểm của mỗi đường.
Suy ra: MN đi qua trung điểm O của EF.
Vậy AC, EF, MN đồng quy tại O.
Câu 14:
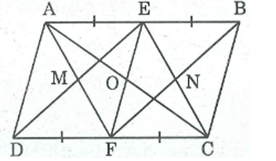
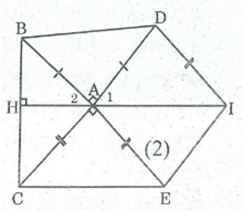
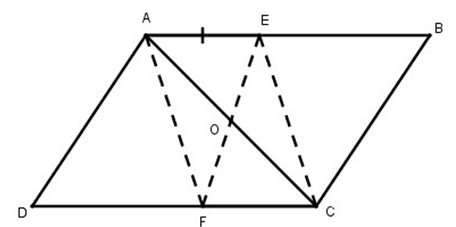
Hình dưới cho ABCD là hình bình hành. Chứng minh rằng: EGFH là hình bình hành.
 Xem đáp án
Xem đáp án
+) Ta có: AH + HD = AD
CG + GB = CB
Mà AD = CB ( vì ABCD là hình bình hành).
DH = GB ( giả thiết)
Suy ra: AH = CG.
Xét AEH và CFG:
AE = CF (gt)
A = C (tính chất hình bình hành)
AH = CG ( chứng minh trên).
Do đó: AEH = CFG (c.g.c)
⇒ EH = FG
Xét BEG và DFH, ta có:
BG = DH (gt)
B = D (tính chất hình bình hành)
BE = DF (vì AB = CD và AE = CF nên AB – AE = CD – CF hay BE = DF )
Do đó: BEG = DFH (c.g.c) ⇒ EG = FH
Suy ra: Tứ giác EGFH là hình bình hành (vì có các cặp cạnh đối bằng nhau)
Câu 15:
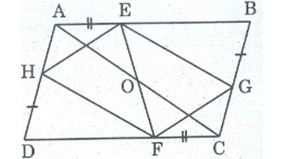
Hình dưới cho ABCD là hình bình hành. Chứng minh rằng: Các đường thẳng AC, BD, EF, GH đồng quy.
 Xem đáp án
Xem đáp án
Gọi O là giao điểm của AC và EF
Xét tứ giác AECF, ta có: AB // CD (gt) hay AE // CF
AE = CF (gt)
Suy ra: Tứ giác AECF là hình bình hành (vì có 1 cặp cạnh đối song song và bằng nhau)
⇒ O là trung điểm của AC và EF
Tứ giác ABCD là hình bình hành có O là trung điểm AC nên O cũng là trung điểm của BD.
Tứ giác EGFH là hình bình hành có O là trung điểm EF nên O cũng là trung điểm của GH.
Vậy AC, BD, EF, GH đồng quy tại O.
Câu 16:
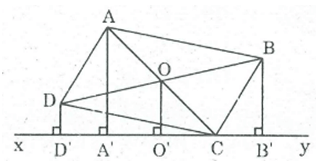
Cho hình hình hành ABCD. Qua C kẻ đường thẳng xy chỉ có một điểm chung C với hình bình hành. Gọi AA', BB', DD' là các đường vuông góc kẻ từ A, B, D đến đường thẳng xy. Chứng minh rằng AA' = BB' + DD'
 Xem đáp án
Xem đáp án
Gọi O là giao điểm của hai đường chéo AC và BD.
Kẻ OO' ⊥ xy
Ta có: BB' ⊥ xy (gt)
DD' ⊥ xy (gt)
Suy ra: BB // OO' // DD'
Tứ giác BB'D'D là hình thang .
OB = OD (t/chất hình bình hành)
Nên O'B' = O'D'
Do đó OO' là đường trung bình của hình thang BB'D'D
⇒ OO' = (BB' + DD') / 2 (tính chất đường trung hình hình thang) (1)
AA' ⊥ xy (gt)
OO' ⊥ xy (theo cách vẽ)
Suy ra: AA' // OO'
Trong ACA' tacó: OA = OC (tính chất hình bình hành)
OO' // AA' nên OO' là đường trung bình của ACA'
⇒ OO' = 1/2 AA' (tính chất đường trung bình của tam giác)
⇒ AA' = 2OO' (2)
Tử (1) và (2) suy ra: AA' = BB' + DD'
Câu 17:
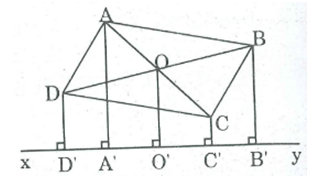
Cho hình bình hành ABCD và đường thẳng xy không có điểm chung với hình bình hành. Gọi AA’; BB’; CC’, DD’ là các đường vuông góc kẻ từ A, B, C, D đến đường thẳng xy. Tìm mối liên hệ độ dài giữa AA', BB', CC', DD'
 Xem đáp án
Xem đáp án
Gọi O là giao điểm của AC và BD
⇒ OA = OC, OB = OD (tính chất hình bình hành)
Kẻ OO' ⊥ xy
AA' ⊥ xy (gt)
CC' ⊥ xy (gt)
Suy ra: AA' // OO' // CC'
Tứ giác ACC'A' là hình thang có:
OA = OC (chứng minh trên)
OO' // AA' nên OO' là đường trung bình của hình thang ACC'A'.
⇒ OO' = (AA' + CC') / 2 (t/chất đường trung bình của hình thang) (1)
BB' ⊥ xy
DD' ⊥ xy (gt)
OO' ⊥ xy (gt)
Suy ra: BB'// OO' // DD'
Tứ giác BDD'B' là hình thang có:
OB = OD (Chứng minh trên)
OO' // BB' nên OO' là đường trung bình của hình thang BDD'B'.
⇒ OO' = (BB' + DD') / 2 (tính chất đường trung bình của hình thang) (2)
Từ (1) và (2) => AA' + CC' = BB + DD'
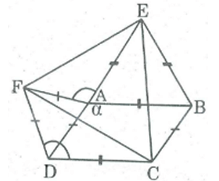
Câu 18:
Cho hình bình hành ABCD có A = α > 90o. Ở phía ngoài hình bình hành vẽ các tam giác đều ADF, ABE. Tính góc (EAF)
 Xem đáp án
Xem đáp án
Vì (BAD) + (BAE) + (EAF) + (FAD) =
⇒ (EAF) = – ((BAD) + (BAE) + (FAD) )
Mà (BAD) = (gt)
(BAE) = (ΔBAE đều)
(FAD) = (ΔFAD đều)
Nên (EAF) = – ( + + ) = –
Câu 19:
Cho hình bình hành ABCD có A = > . Ở phía ngoài hình bình hành vẽ các tam giác đều ADF, ABE. Chứng minh rằng tam giác CEF là tam giác đều.
 Xem đáp án
Xem đáp án
Ta có:
(BAD) + ∠(ADC) = (hai góc trong cùng phía bù nhau)
⇒ (ADC) = - (BAD) = –
(CDF) = (ADC) + (ADF) = -
Suy ra: (CDF) = (EAF)
Xét AEF và DCF: AF = DF ( vì ADF đều)
AE = DC (vì cùng bằng AB)
(CDF) = (EAF) (chứng minh trên)
Do đó: AEF = DCF (c.g.c) ⇒ EF = CF (1)
(CBE) = (ABC) +
Xét ΔBCE và ΔDFC: BE = CD ( vì cùng bằng AB)
(CBE) = (CDF) =
BC = DF (vì cùng bằng AD)
Do đó BCE = DFC (c.g.c) ⇒ CE = CF (2)
Từ (1) và (2) suy ra: EF = CF = CE
Vậy ECF đều.
Câu 20:
Cho tam giác ABC. Ở phía ngoài tam giác vẽ các tam giác vuông cân tại A là ABD, ACE. Vẽ hình bình hành ADIE. Chứng minh rằng: IA = BC
 Xem đáp án
Xem đáp án
(BAD) + (BAC) + (DAE) + (EAC) =
Lại có: (BAD) = , (EAC) =
Suy ra: (BAC) + (DAE) = (1)
AE // DI (gt)
⇒ (ADI) + (DAE) = (2 góc trong cùng phía)
Từ (1) và (2) suy ra: (BAC) = (ADI)
Xét ABC và DAI có:
AB = AD ( vì tam giác ABD vuông cân).
AC = DI ( = AE)
(BAC) = (ADI) ( chứng minh trên)
Suy ra: ABC = DAI (c.g.c) ⇒ IA = BC
Câu 21:
Cho tam giác ABC. Ở phía ngoài tam giác vẽ các tam giác vuông cân tại A là ABD, ACE. Vẽ hình bình hành ADIE. Chứng minh rằng: IA ⊥ BC
 Xem đáp án
Xem đáp án
ABC = DAI (chứng minh trên) ⇒ (ABC) = (3)
Gọi giao điểm IA và BC là H.
Ta có: + (BAD) + = (kề bù)
Mà (BAD) = (gt) ⇒ + = (4)
Từ (3) và (4) suy ra: (ABC)+ =
Trong AHB ta có: (AHB) + (ABC)+ =
Suy ra (AHB) = ⇒ AH ⊥ BC hay IA ⊥ BC
Câu 22:
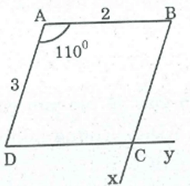
Dựng hình bình hành ABCD biết: AB = 2cm, AD = 3cm, A =
 Xem đáp án
Xem đáp án
Cách dựng
- Dựng ΔABD có AB = 2cm, ∠A = 110o, AD = 3cm
- Dựng tia Bx //AD
- Dựng tia Dy // AB và Dy cắt Bx tại C
Ta có hình bình hành ABCD cần dựng
Chứng minh
AB //CD, AD // BC nên tứ giác ABCD là hình bình hành.
Ta lại có: AB = 2cm, A = , AD = 3cm.
Bài toán có một nghiệm hình.
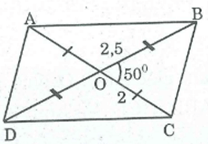
Câu 23:
Dựng hình bình hành ABCD biết: AC = 4cm, BD = 5cm, (BOC) =
 Xem đáp án
Xem đáp án
Cách dựng
- Dựng OBC có OC = 2cm, OB = 2,5 cm, (BOC) =
- Trên tia đối tia OC lấy điểm A sao cho OA = OC = 2cm
- Trên tia đối tia OB lấy điểm D sao cho OD = OB =2,5cm
Nối AB, BC, CD, AD ta có hình bình hành ABCD cần dựng
Chứng minh
Tứ giác ABCD có OA = OC, OB = OD nên nó là hình bình hành vì có 2 đường chéo cắt nhau tại trung điểm mỗi đường.
Có AC = 4cm , BD = 5cm, (BOC) =
Bài toán có một nghiệm hình
Câu 24:
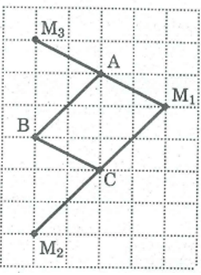
Cho ba điểm A, B, C trên giấy kẻ ô vuông ở hình bên. Hãy vẽ điểm thứ tư M sao cho A, B,C, M là 4 đỉnh của một hình bình hành.
 Xem đáp án
Xem đáp án
- Nếu hình bình hành nhận AC làm đường chéo vì AB là đường chéo hình vuông có 2 ô vuông nên C là đường chéo hình vuông cạnh 2 ô vuông và A, nằm trên một nửa mặt phẳng bờ BC ta có hình bình hành ABC
- Nếu hình bình hành nhận BC làm đường chéo, điểm A cách điểm C ba ô vuông, điểm B cách điểm là ba ô vuông và trên một nửa mặt phẳng bờ AB ta có hình bình hành ABC
- Nếu hình bình hành nhận AB làm đường chéo thì điểm cách điểm B ba ô vuông, và A nằm trên cùng một nửa mặt phẳng bờ BC ta có hình bình hành ACB
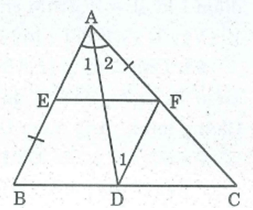
Câu 25:
Cho tam giác ABC. Dựng đường thẳng song song với BC, cắt cạnh AB ở E, cắt cạnh AC ở F sao cho BE = AF
 Xem đáp án
Xem đáp án
Cách dựng:
- Dựng đường phân giác AD của góc BAC.
- Qua D dựng đường thẳng song song AB cắt AC tại F.
- Qua F dựng đường thẳng song song với BC cắt AB tại E.
Ta có điểm E, F cần dựng.
Chứng minh:
DF // AB
⇒ = (so le trong)
Lại có: = ( vì AD là tia phân giác của góc BAC).
Suy ra: =
⇒ AFD cân tại F ⇒ AF = DF (l)
DF // AB hay DF // BE
EF // BC hay EF // BD
Tứ giác BDFE là hình bình hành ⇒ BE = DF (2)
Từ (1) và (2) suy ra: AF = BE.
Câu 26:
Tứ giác ABCD là hình bình hành nếu:
A. AB = CD;
B. AD = BC;
C. AB // CD và AD = BC;
D. AB = CD và AD = BC.
Hãy chọn phương án đúng.
 Xem đáp án
Xem đáp án
Chọn D
Câu 27:
Cho hình bình hành ABCD , các đường chéo cắt nhau tại O. Gọi E, F theo thứ tự là trung điểm của OD, OB. Gọi K là giao điểm của AE và CD. Chứng minh rằng: AE song song CF
 Xem đáp án
Xem đáp án
Ta có: OB = OD (tính chất hình bình hành)
OE = 1/2 OD (gt)
OF = 1/2 OB (gt)
Suy ra: OE = OF
Xét tứ giác AECF, ta có:
OE = OF (chứng minh trên)
OA = OC (vì ABCD là hình bình hành)
Suy ra: Tứ giác AECF là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm mỗi đường ) ⇒ AE // CF
Câu 28:
Cho hình bình hành ABCD , các đường chéo cắt nhau tại O. Gọi E, F theo thứ tự là trung điểm của OD, OB. Gọi K là giao điểm của AE và CD. Chứng minh rằng: DK = 1/2 KC
 Xem đáp án
Xem đáp án
Kẻ OM // AK
Trong CAK ta có:
OA = OC ( chứng minh trên)
OM // AK ( theo cách vẽ)
⇒ CM = MK (tính chất đường trung bình của tam giác) (1)
Trong DMO ta có:
DE = EO (gt)
EK // OM (vì AK // OM)
⇒ DK = KM (tính chất đường trung bình của tam giác) (2)
Từ (1) và (2) suy ra: DK = KM = MC ⇒ DK = 1/2 KC
Câu 29:
Cho hình bình hành ABCD. Lấy điểm E trên cạnh AB, điểm F trên cạnh CD sao cho AE = CF. Chứng minh rằng ba đường thẳng AC, BD, EF đồng quy.
 Xem đáp án
Xem đáp án
Gọi O là giao điểm của hai đường chéo AC và BD.
Xét tứ giác AECF:
AB // CD (gt)
⇒ AE // CF
AE = CF (gt)
Suy ra: Tứ giác AECF là hình bình hành ( vì có một cặp cạnh đối song song và bằng nhau)
⇒ AC và EF cắt nhau tại trung điểm mỗi đường
OA = OC ( tính chất hình bình hành) ⇒ EF đi qua O
Vậy AC, BD, EF đồng quy tại O.