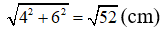- Đề số 1
- Đề số 2
- Đề số 3
- Đề số 4
- Đề số 5
- Đề số 6
- Đề số 7
- Đề số 8
- Đề số 9
- Đề số 10
- Đề số 11
- Đề số 12
- Đề số 13
- Đề số 14
- Đề số 15
- Đề số 16
- Đề số 17
- Đề số 18
- Đề số 19
- Đề số 20
- Đề số 21
- Đề số 22
- Đề số 23
- Đề số 24
- Đề số 25
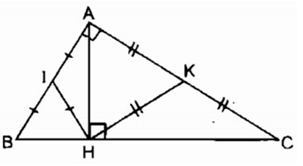
- Đề số 26
- Đề số 27
- Đề số 28
- Đề số 29
- Đề số 30
- Đề số 31
- Đề số 32
- Đề số 33
- Đề số 34
- Đề số 35
- Đề số 36
- Đề số 37
- Đề số 38
- Đề số 39
- Đề số 40
- Đề số 41
Bài 9: Toán 8 Hình chữ nhật
-
7189 lượt thi
-
26 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
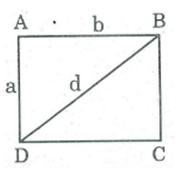
Tính đường chéo d của một hình chữ nhật, biết các cạnh a = 3cm, b = 5cm (làm tròn kết quả đến chữ số thập phân thứ nhất).
 Xem đáp án
Xem đáp án
Giả sử hình chữ nhật ABCD có AB = b = 5cm; AD= a = 3cm; BD = d.
Áp dụng định lí Pi-ta-go vào tam giác vuông ABD, ta có:
⇒ = 9 + 25 = 34
Vậy 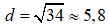
Câu 2:
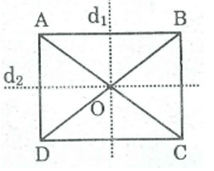
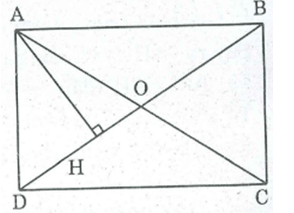
Chứng minh rằng trong hình chữ nhật: Giao điểm của hai đường chéo là tâm đối xứng của hình.
 Xem đáp án
Xem đáp án
Gọi O là giao điểm hai đường chéo AC và BD.
Vì ABCD là hình chữ nhật nên ABCD cũng là hình bình hành.
Do đó, O là trung điểm của AC và BD.
Suy ra, điểm O là tâm đối xứng của nó.
Câu 3:
Chứng minh rằng trong hình chữ nhật: Hai đường thẳng đi qua trung điểm, của hai cạnh đối là trục đối xứng của hình.
 Xem đáp án
Xem đáp án
Trong hình thang cân, đường thẳng đi qua trung điểm của hai đáy là trục đối xứng của nó.
Theo định nghĩa ta có hình chữ nhật cũng là một hình thang cân. Nếu ta xem hình chữ nhật ABCD là hình thang cân có hai cạnh đáy AB và CD thì đường thẳng đi qua trung điểm của AB và CD là trục đối xứng của hình chữ nhật ABCD.
Nếu ta xem hình chữ nhật ABCD là hình thang cân có hai cạnh đáy AD và BC thì đường thẳng đi qua trung điểm của AD và BC là trục đối xứng của hình chữ nhật ABCD.
Câu 4:
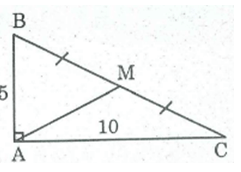
Tính độ dài đường trung tuyến ứng với cạnh huyền của một tam giác vuông có các cạnh góc vuông bằng 5cm và 10cm. (làm tròn kết quả đến chữ số thập phân thứ nhất)
 Xem đáp án
Xem đáp án
Giả sử tam giác ABC có A = , M trung điểm BC; AB = 5cm, AC = 10cm
Áp dụng định lý Pi-ta-go vào tam giác vuông ABC, ta có:
BC = ≈ 11,2 (cm)
Mà AM = 1/2 BC (tính chất tam giác vuông)
⇒ AM = 1/2 .11,2 = 5,6 (cm)
Câu 5:
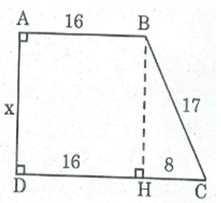
Tính x trong hình dưới
 Xem đáp án
Xem đáp án
Kẻ BH ⊥ CD,ta có: A = , D = , (BHD) =
Suy ra tứ giác ABHD là hình chữ nhật (vì có ba góc vuông)
⇒ AB = DH = 16, BH = AD
HC = CD – DH = CD – AB = 24 – 16 = 8 (cm)
Trong tam giác vuông BHC, theo định lý Pi-ta-go, ta có:
⇒ BH2 = BC2 - HC2
= 289 – 64 = 225
BH = = 15 (cm)
Vậy x = AD = BH = 15 (cm).
Câu 6:
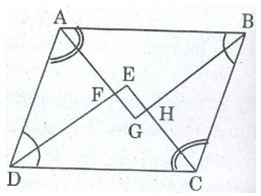
Chứng minh rằng các tia phân giác các góc của hình bỉnh hành cắt nhau tạo thành một hình chữ nhật.
 Xem đáp án
Xem đáp án
Gọi G, H, E, F lần lượt là giao điểm của các đường phân giác của A và B; B và C; C và D; D và A
Ta có: (ADF) = 1/2 (ADC) (gt)
(DAF) = 1/2 (DAB) (gt)
(ADC) + (DAB) = (hai góc trong cùng phía)
Suy ra: (ADF) + (DAF) = 1/2 ((ADC) + (DAB) ) = 1/2 . =
Trong AFD, ta có:
(AFD) = – ((ADF) + (DAF)) = – =
(EFG) = (AFD) (đối đỉnh)
⇒ (EFG) =
(GAB) = 1/2 (DAB) (gt)
(GBA) = 1/2 (CBA) (gt)
(DAB) + (CBA) = (hai góc trong cùng phía)
⇒ (GAB) + (GBA) = 1/2 ((DAB) + (CBA) ) = 1/2 . =
Trong ΔAGB ta có: (AGB) = – ((GAB) + (GBA) ) = - =
Hay G =
(EDC) = 1/2 (ADC) (gt)
(ECD) = 1/2 (BCD) (gt)
(ADC) + (BCD) = (hai góc trong cùng phía)
⇒ (EDC) + (ECD) = 1/2 (∠ADC) + (BCD) ) = 1/2 . =
Trong ΔEDC ta có: (DEC) = – ((EDC) + (ECD) ) = - =
Hay E =
Vậy tứ giác EFGH là hình chữ nhật (vì có ba góc vuông).
Câu 7:
Tứ giác ABCD có hai đường chéo vuông góc với nhau. Gọi E, F, G, H theo thứ tự là trung điểm của AB, BC, CD, DA. Tứ giác EFGH là hình gì? Vì sao?
 Xem đáp án
Xem đáp án
* Trong ABC, ta có:
E là trung điểm của AB (gt)
F là trung điểm của BC (gt)
Nên EF là đường trung bình của ABC
⇒ EF // AC và EF = 1/2 AC (tính chất đường trung bình tam giác) (1)
* Trong DAC, ta có:
H là trung điểm của AD (gt)
G là trung điểm của DC (gt)
Nên HG là đường trung bình của DAC.
⇒ HG // AC và HG = 1/2 AC (tính chất đường trung bình tam giác) (2)
Từ (1) và (2) suy ra: EF // HG và EF = HG
Suy ra tứ giác EFGH là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau)
Ta lại có: BD ⊥ AC (gt)
EF // AC (chứng minh trên)
Suy ra: EF ⊥ BD
Trong ABD ta có EH là đường trung bình ⇒ EH // BD
Suy ra: EF ⊥ EH hay (FEH) =
Vậy hình bình hành EFGH là hình chữ nhật.
Câu 8:
Tìm các hình chữ nhật trong hình vẽ sau.
 Xem đáp án
Xem đáp án
* B = (HDC)
⇒ AB // DH (vì có cặp góc đồng vị bằng nhau)
Hay DH //AE
* C = (BDE)
⇒ DE // AC (vì có cặp góc đồng vị bằng nhau)
Hay DE //AH
Vậy tứ giác AHDE là hình bình hành ( có các cặp đối song song với nhau )
Mà A = nên AHDE là hình chữ nhật
Câu 9:
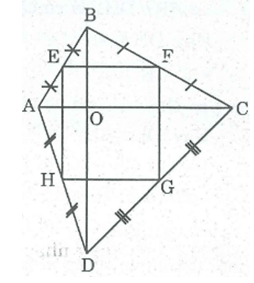
Tìm các hình chữ nhật trong hình vẽ sau
 Xem đáp án
Xem đáp án
Tứ giác MNPQ có:
OM = OP = R nên O là trung điểm của MP
ON = OQ = R nên O là trung điểm của NQ
Tứ giác MNPQ có O là trung điểm của mỗi đường chéo
Suy ra:Tứ giác MNPQ là hình bình hành
Lại có: MP = NQ = 2R ( = đường kính của đường tròn)
Nên tứ giác MNPQ là hình chữ nhật
Câu 10:
Các câu sau đúng hay sai?
a. Hình chữ nhật là tứ giác có tất cả các góc bằng nhau.
b. Tứ giác có hai đường chéo bằng nhau là hình chữ nhật.
c. Tứ giác có hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường là hình chữ nhật.
 Xem đáp án
Xem đáp án
a. Đúng vì hình chữ nhật có 4 góc vuông.
b. Sai vì hình thang cân có 2 cạnh bên không song song có 2 đường chéo bằng nhau nhưng hình thang cân đó không là hình chữ nhật.
c. Đúng vì:
Tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường là hình bình hành.
Hình bình hành có hai đường chéo bằng nhau là hình chữ nhật.
Câu 11:
Cho tam giác ABC vuông cân tại A, AC = 4cm, điểm M thuộc cạnh BC. Gọi D, E theo thứ tự là chân đường vuông góc kẻ từ M đến AB, AC. Tứ giác ADME là hình gì? Tính chu vi của tứ giác đó
 Xem đáp án
Xem đáp án
Xét tứ giác ADME, ta có:
A= (gt)
MD ⊥ AB (gt)
⇒ (ADM) =
Lại có, MD ⊥ AC ⇒ (MEA) =
Suy ra tứ giác ADME là hình chữ nhật (vì có 3 góc vuông)
ABC vuông cân tại A ⇒ B = và AB = AC = 4cm
Suy ra: DBM vuông cân tại D
⇒ DM = DB
Chu vi hình chữ nhật ADME bằng:
2(AD + DM) = 2(AD + DB) = 2AB = 2.4 = 8 (cm)
Câu 12:
Cho tam giác ABC vuông cân tại A, AC = 4cm, điểm M thuộc cạnh BC. Gọi D, E theo thứ tự là chân đường vuông góc kẻ từ M đến AB, AC. Điểm M ở vị trí nào trên BC thì đoạn DE có độ dài nhỏ nhất.
 Xem đáp án
Xem đáp án
Gọi H là trung điểm của BC
Suy ra: AH ⊥ BC (tính chất tam giác cân)
Do đó, AM AH ( quan hệ đường vuông góc và đường xiên )(dấu " = " xảy ra khi M trùng với H)
Tứ giác ADME là hình chữ nhật .
⇒ AM = DE (tính chất hình chữ nhật)
Suy ra: DE AH
Vậy DE có độ dài nhỏ nhất là AH khi và chỉ khi điểm M là trung điểm của BC.
Câu 13:
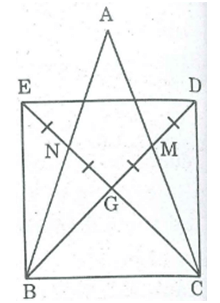
Cho tam giác ABC cân tại A, các đường trung tuyến BM, CN cắt nhau tại G. Gọi D là điểm đối xứng với G qua M, gọi E là điểm đối xứng với G qua N. Tứ giác BEDC là hình gì? Vì sao?
 Xem đáp án
Xem đáp án
* Tam giác ABC có hai đường trung tuyến BM và CN cắt nhau tại G
Suy ra: G là trọng tâm của ABC .
⇒ GB = 2GM (tính chất đường trung tuyến)
GC = 2GN (tính chất đường trung tuyến)
Điểm D đối xứng với điểm G qua điểm M
⇒ MG = MD hay GD = 2GM
Suy ra: GB = GD (l)
Điểm E đối xứng với điểm G qua điểm N
⇒ NG = NE hay GE = 2GN
Suy ra: GC = GE (2)
Từ (1) và (2) suy ra tứ giác BCDE là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm mỗi đường)
Xét BCM và CBN, có: BC cạnh chung
(BCM) = (CBN) (tính chất tam giác cân)
CM = BN (vì AB = AC)
Suy ra: BCM = CBN (c.g.c)
⇒ (MBC) = (NCB) ⇒ GBC cân tại G ⇒ GB = GC ⇒ BD = CE
Hình bình hành BCDE có hai đường chéo bằng nhau nên nó là hình chữ nhật.
Câu 14:
Cho hình chữ nhật ABCD. Gọi H là chân đường vuông góc kẻ từ A đến BD. Biết HD = 2cm, HB = 6cm. Tính độ dài AD, AB (làm tròn đến hàng đơn vị).
 Xem đáp án
Xem đáp án
Ta có:
DB = HD + HB = 2 + 6 = 8 (cm)
AC = DB (tính chất hình chữ nhật)
OA = OB = OC = OD = 1/2 BD = 4 (cm)
OD = OH + HD
⇒ OH = OD – HD = 4 – 2 = 2 (cm)
Suy ra: OH = HD = 2 cm nên H là trung điểm của OD
Tam giác ADO có AH là đường cao đồng thời là đường trung tuyến nên tam giác ADO cân tại A
⇒AD = AO = 4 (cm)
Trong tam giác vuông ABD có (BAD) =
(định lý Pi-ta-go) ⇒
AB = ≈ 7 (cm).
Câu 15:
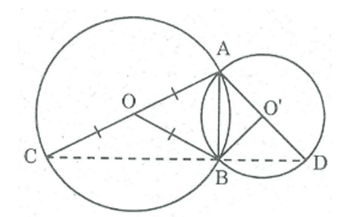
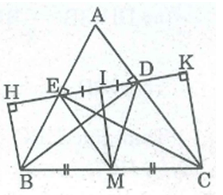
Chứng minh rằng ba điểm C, B, D ở hình dưới thẳng hàng.
 Xem đáp án
Xem đáp án
Nối AB, BO, BC, BO', BD.
* Trong ABC, ta có: OA = OC = R (bán kính đường tròn (O))
Nên BO là đường trung tuyến của ABC.
Mà BO = R (bán kính (O)) ⇒ BO = OA= OC = 1/2 AC
Suy ra tam giác ABC vuông tại B ⇒ (ABC) =
* Trong ABD , ta có: AO' = O'D = R' (bán kính đường tròn (O'))
Nên BO' là đường trung tuyến của tam giác ABD.
Mà BO' = R' (bán kính (O')) ⇒ BO' = AO' = O'D = 1/2 AD
Suy ra tam giác ABD vuông tại B ⇒ (ABD) =
Ta có: (ABC) + (ABD) = (CBD) = + =
Vậy C, B, D thẳng hàng.
Câu 16:
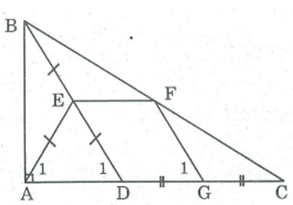
Tứ giác ABCD có AB ⊥ CD. Gọi E, F, G, H theo thứ tự là trung điểm của BC, BD, AD, AC. Chứng minh rằng EG = FH.
 Xem đáp án
Xem đáp án
* Trong BCD, ta có:
E là trung điểm của BC (gt)
F là trung điểm của BD (gt)
Suy ra EF là đường trung bình của BCD
⇒ EF // CD và EF = 1/2 CD (1)
* Trong ACD, ta có: H là trung điểm của AC (gt)
G là trung điểm của AD (gt)
Suy ra HG là đường trung bình của ACD
⇒HG // CD và HG = 1/2 CD (2)
Từ (1) và (2) suy ra: EF // HG và EF = HG
Suy ra tứ giác EFGH là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau).
* Mặt khác: EF // CD (chứng minh trên)
AB ⊥ CD (gt)
Suy ra EF ⊥ AB
Trong ABC ta có HE là đường trung bình ⇒ HE // AB
Suy ra: HE ⊥ EF hay (FEH) =
Vậy hình bình hành EFGH là hình chữ nhật.
Câu 17:
Cho tam giác ABC, đường cao AH. Gọi D, E, M theo thứ tự là trung điểm của AB, AC, BC. Chứng minh rằng tứ giác DEMH là hình thang cân.
 Xem đáp án
Xem đáp án
* Vì D trung điểm của AB (gt) và E trung điểm của AC (gt) nên DE là đường trung bình của tam giác ABC
⇒ DE // BC hay DE // HM
Suy ra tứ giác DEMH là hình thang
* Mà M trung điểm BC (gt) nên DM là đường trung bình của BAC
⇒ DM = 1/2 AC (tính chất đường trung bình của tam giác) (1)
* Trong tam giác vuông AHC có (AHC) = . HE là đường trung tuyến ứng với cạnh huyền AC.
⇒ HE = 1/2 AC (tính chất tam giác vuông) (2)
Từ (1) và (2) suy ra: DM = HE
Vậy hình thang DEMH là hình thang cân (vì có 2 đường chéo DM và EH bằng nhau).
Câu 18:
Cho tam giác ABC vuông tại A, điểm D thuộc cạnh AC. Gọi E, F, G theo thứ tự là trung điểm của BD, BC, DC. Chứng minh rằng tứ giác AEFG là hình thang cân.
 Xem đáp án
Xem đáp án
* Trong BDC, ta có:
E là trung điểm của BD (gt)
F là trung điểm của BC (gt)
Suy ra EF là đường trung bình của tam giác BCD
⇒ EF // DC hay EF // AG
Suy ra tứ giác AEFG là hình thang
G là trung điểm của DC (gt)
Nên FG là đường trung bình của tam giác BCD
⇒ FG // BD ⇒ = ∠(đồng vị) (1)
* Trong tam giác ABD vuông tại A có AE là đường trung tuyến ứng với cạnh huyền BD
⇒ AE = ED = 1/2 BD (tính chất tam giác vuông)
Suy ra: tam giác AED cân tại E nên = (2)
Từ (1) và (2) suy ra: =
Vậy hình thang AEFG là hình thang cân.
Câu 19:
Cho tam giác nhọn ABC, các đường cao BD, CE. Gọi H, K theo thứ tự là chân đường vuông góc kẻ từ B, C đến đường thẳng DE. Chứng minh rằng EH = DK.
 Xem đáp án
Xem đáp án
* Ta có: BH ⊥ DE (gt)
CK ⊥ DE (gt)
⇒ BH // CK hay tứ giác BHKC là hình thang
Gọi M là trung điểm của BC, I là trung điểm của DE
* Trong tam giác BDC vuông tại D có DM là trung tuyến ứng với cạnh huyền BC.
⇒ DM = 1/2 BC (tính chất tam giác vuông)
* Trong tam giác BEC vuông tại E có EM là đường trung tuyến ứng với cạnh huyền BC.
⇒ EM = 1/2 BC (tính chất tam giác vuông)
Suy ra: DM = EM nên ΔMDE cân tại M
MI là đường trung tuyến nên MI là đường cao ⇒ MI ⊥ DE
Suy ra: MI // BH // CK
BM = MC
Suy ra: HI = IK (tính chất đường trung bình hình thang)
⇒ HE + EI = ID + DK
Mà EI = ID nên EH = DK
Câu 20:
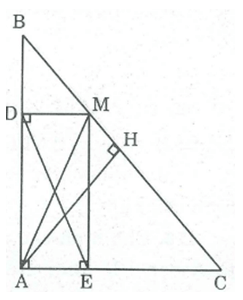
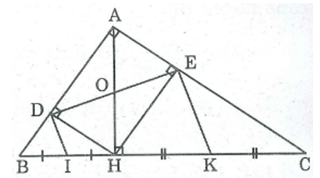
Cho tam giác ABC vuông tại A, đường cao AH. Gọi D, E theo thứ tự là chân đường vuông góc kể từ H đến AB, AC. Chứng minh rằng AH = DE
 Xem đáp án
Xem đáp án
Xét tứ giác ADHE, ta có:
A = (gt)
(ADH) = (vì HD ⊥ AB)
(AEH) = (Vì HE ⊥ AC)
Suy ra tứ giác ADHE là hình chữ nhật (vì có 3 góc vuông)
Vậy AH = DE (tính chất hình chữ nhật)
Câu 21:
Cho tam giác ABC vuông tại A, đường cao AH. Gọi D, E theo thứ tự là chân đường vuông góc kể từ H đến AB, AC. Gọi I là trung điểm của HB, K là trung điểm của HC. Chứng minh rằng DI // EK
 Xem đáp án
Xem đáp án
Tam giác BDH vuông tại D có DI là đường trung tuyến thuộc cạnh huyền BH
⇒ DI = IB = 1/2 BH (tính chất tam giác vuông)
⇒ IDB cân tại I ⇒ (DIB) = - 2.B (1)
Tam giác HEC vuông tại E có EK là đường trung tuyến thuộc cạnh huyền HC.
⇒ EK = KH = 1/2 HC (tính chất tam giác vuông) .
⇒ KHE cân tại K ⇒ (EKH) = - 2.(KHE) (2)
Tứ giác ADHE là hình chữ nhật nên:
HE // AD hay HE // AB ⇒ B = (KHE) (đồng vị)
Từ (1), (2) và (3) suy ra: (DIB) = (EKH)
Vậy DI // EK (vì có cặp góc đồng vị bằng nhau).
Câu 22:
Cho tam giác ABC vuông tại A, đường cao AH, đường trung tuyến AM. Chứng minh rằng (HAB) = (MAC)
 Xem đáp án
Xem đáp án
Ta có: AH ⊥ BC (gt) ⇒ (HAB) + B =
Lại có: B + C = (vì ABC có ∠A = )
Suy ra (HAB) = C (1)
ABC vuông tại A có AM là trung tuyến thuộc cạnh huyền BC
⇒ AM = MC = 1/2 BC (tính chất tam giác vuông)
⇒ MAC cân tại M ⇒ (MAC) = C (2)
Từ (1) và (2) suy ra: (HAB) = (MAC)
Câu 23:
Cho tam giác ABC vuông tại A, đường cao AH, đường trung tuyến AM. Gọi D, E theo thứ tự là chân đường vuông góc kể từ H đến AB, AC. Chứng minh rằng AM vuông góc với DE.
 Xem đáp án
Xem đáp án
Xét tứ giác ADHE, ta có:
A = (gt)
(ADH) = (vì HD ⊥ AB)
(AEH) = (vì HE ⊥ AC)
Suy ra tứ giác ADHE là hình chữ nhật (vì có 3 góc vuông).
+ Xét ADH và EHD có :
DH chung
AD = EH ( vì ADHE là hình chữ nhật)
(ADN) = (EHD) =
Suy ra: ADH = EHD (c.g.c)
⇒ = (HED)
Lại có: (HED) + = (HEA) =
Suy ra: + =
= ∠(chứng minh trên) ⇒ + =
Gọi I là giao điểm của AM và DE.
Trong AIE ta có: (AIE) = 180o – (+ ) = - =
Vậy AM ⊥ DE.
Câu 24:
Một hình chữ nhật có hai cạnh kề bằng nhau 4cm và 6cm. Độ dài đường chéo của hình chữ nhật đó bằng bao nhiêu xentimét ?
A. 8cm
B. cm
C. 9cm
D. cm
Hãy chọn phương án đúng.
 Xem đáp án
Xem đáp án
Độ dài đường chéo của hình chữ nhật là:
Chọn B
Câu 25:
Cho tam giác ABC vuông tại A, đường cao AH. Gọi I, K theo thứ tự là trung điểm của AB, AC. Tính số đo góc IHK.
 Xem đáp án
Xem đáp án
ΔAHB vuông tại H có HI là đường trung tuyến thuộc cạnh huyền AB
⇒ HI = IA = 1/2 AB (tính chất tam giác vuông)
⇒ AHI cân tại I
⇒ (IAH) = (IHA) (1)
AHC vuông tại H có HK là đường trung tuyến thuộc cạnh huyền AC
⇒ HK = KA = 1/2 AC (tính chất tam giác vuông)
⇒ KAH cân tại K ⇒(KAH) = (KHA) (2)
(IHK) = (IHA) + (KHA) (3)
Từ (1), (2) và (3) suy ra: (IHK) = (IAH) + (KAH) = (IAK) = (BAC) =
Câu 26:
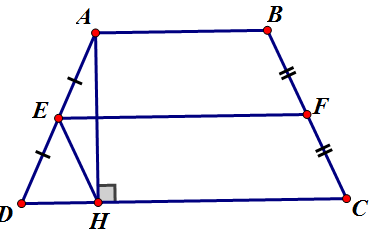
Cho hình thang cân ABCD, đường cao AH. Gọi E, F theo thứ tự là trung điểm của các cạnh bên AD, BC. Chứng minh rằng EFCH là hình bình hành.
 Xem đáp án
Xem đáp án
*Có AH ⊥ CD ⇒ AHD vuông tại H
E là trung điểm của AD ⇒ HE là trung tuyến ứng với cạnh huyền AD
⇒ HE = 1/2 AD (1)
*F là trung điểm của BC ⇒ CF = 1/2 BC (2)
Mà ABCD là hình thang cân ⇒ BC = AD (3)
Từ (1), (2) và (3) ta có: HE = CF (*)
*Mặt khác: EH = ED = 1/2 AD (Chứng minh trên)
⇒ EHD cân tại E
⇒ (EHD) = (EDH)
Mà (EDH) = (FCH) (góc đáy hình thang cân)
⇒ (FCH) = (EHD) (cùng bằng (EDH))
⇒EH // FC (2 góc ở vị trí đồng vị bằng nhau) (**)
Từ (*) và (**) ⇒ EFCH là hình bình hành (1 cặp cạnh song song và bằng nhau)