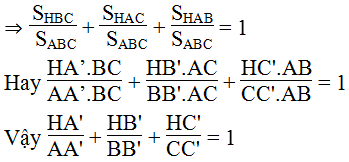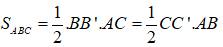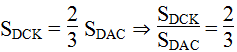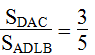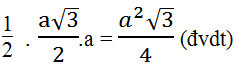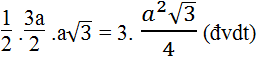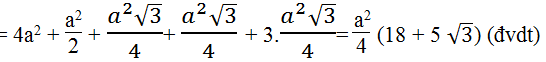21 câu hỏi trắc nghiệm thuộc Ôn tập chương 2 - Phần Hình học

Giải Sách Bài Tập Toán 8 Tập 1

Đề số 1
Đề số 2
Đề số 3
Đề số 4
Đề số 5
Đề số 6
Đề số 7
Đề số 8
Đề số 9
Đề số 10
Đề số 11
Đề số 12
Đề số 13
Đề số 14
Đề số 15
Đề số 16
Đề số 17
Đề số 18
Đề số 19
Đề số 20
Đề số 21
Đề số 22
Đề số 23
Đề số 24
Đề số 25
Đề số 26
Đề số 27
Đề số 28
Đề số 29
Đề số 30
Đề số 31
Đề số 32
Đề số 33
Đề số 34
Đề số 35
Đề số 36
Đề số 37
Đề số 38
Đề số 39
Đề số 40
Đề số 41

Ôn tập chương 2 - Phần Hình học

7186 lượt thi
21 câu hỏi
30 phút

Danh sách câu hỏi

Câu 1:

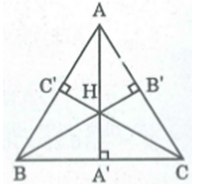
Cho tam giác ABC với ba đường cao AA’, BB’, CC’. Gọi H là trực tâm của tam giác đó. Chứng minh rằng $\frac{H A'}{A A'} + \frac{H B'}{B B'} + \frac{H C'}{C C'} = 1$

Xem đáp án

Ta có: $S_{H B C} + S_{H A C} + S_{H A B} = S_{A B C}$

Câu 2:

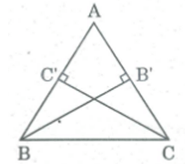
Cho tam giác ABC. Tính tỉ số đường cao BB’, CC’ xuất phát từ đỉnh B, C

Xem đáp án

Ta có:

Suy ra: BB'.AC = CC'.AB

Câu 3:

Cho tam giác ABC. Tại sao nếu AB < AC thì BB' < CC'

Xem đáp án

Vậy BB' < CC'.

Câu 4:

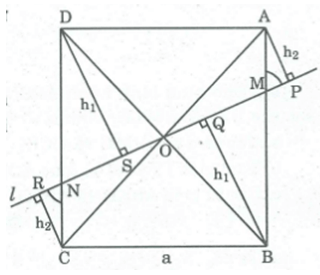
Qua tâm O của hình vuông ABCD cạnh a, kẻ đường thắng l cắt cạnh AB và CD lần lượt tại M và N. Biết MN = b. Hãy tính tổng các khoảng cách từ các đỉnh của hình vuông đến đường thẳng l theo a và b (a và b có cùng đơn vị đo).

Xem đáp án

Gọi $h_{1}$ và $h_{2}$ là khoảng cách từ đỉnh B và đỉnh A đến đường thẳng l

Tổng khoảng cách là S.

Vì O là tâm đối xứng của hình vuông nên OM = ON (tính chất đối xứng tâm)

Suy ra AM = CN

Mà: $∠$ (AMP) = $∠$ (DNS) (đồng vị)

$∠$ (DNS) = $∠$ (CNR) (đôi đỉnh)

Suy ra: $∠$ (AMP) = $∠$ (CNR)

Suy ra: $∆$ APM = $∆$ CRN (cạnh huyền, góc nhọn)

⇒ CR = AP = $h_{2}$

AM = CN ⇒ BM = DR

$∠$ (BMQ) = $∠$ (DNS) (so le trong)

Suy ra: $∆$ BQM = $∆$ DSN (cạnh huyền, góc nhọn) ⇒ DS = BQ = $h_{1}$

$S_{B O A} = 1 / 4 S_{A O B} = 1 / 4 a^{2}$ (l)

$S_{B O A} = S_{B O M} + S_{A O M}$ = 1/2 .b/2 . $h_{1}$ + 1/2 .b/2 . $h_{2}$

Từ (1) và (2) suy ra $h_{1}$ + $h_{2}$ = $a^{2}$ b . Vậy : S = 2( $h_{1}$ + $h_{2}$ ) = 2 $a^{2}$ b

Câu 5:

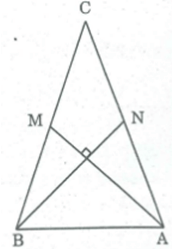
Tam giác ABC có hai trung tuyến AM, BN vuông góc với nhau. Hãy tính diện tích tam giác đó theo AM và BN.

Xem đáp án

Tứ giác ẠBMN có hai đường chéo vuông góc.

Ta có: $S_{A B M N}$ = 1/2 AM.BN

$∆$ ABM và $∆$ AMC có chung chiều cao kể từ A, cạnh đáy BM = MC nên: $S_{A B M}$ = $S_{A M C}$ = 1/2 $S_{A B C}$

$∆$ MNA và $∆$ MNC có chung chiều cao kê từ M, cạnh đáy AN = NC nên: $S_{M A N}$ = $S_{M N C}$ = 1/2 $S_{A M C}$ = 1/4 $S_{A B C}$

$S_{A B M N}$ = $S_{A B M}$ + $S_{M N A}$ = 1/2 $S_{A B C}$ + 1/4 $S_{A B C}$ = 3/4 $S_{A B C}$

Vậy $S_{A B C}$ = 4/3 $S_{A B M N}$ = 4/3 .1/2 .AM.BN = 2/3 AM.BN

Câu 6:

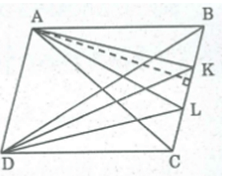
Cho hình bình hành ABCD. Gọi K và L là hai điểm thuộc BC sao cho BK = KL = LC. Tính tỉ số diện tích của: Các tam giác DAC và DCK

Xem đáp án

Ta có: $S_{A C D}$ = $S_{B C D}$ = $S_{D A B}$ = $S_{D A B}$ = 1/2 $S_{A B C D}$ (1)

$∆$ DCK và $∆$ DCB có chung chiều cao kẻ từ đỉnh D, cạnh đáy CK = 2/3 CB

$S_{D C K}$ = 2/3 $S_{D B C}$ (2)

Từ (1) và (2) ⇒

Câu 7:

Cho hình bình hành ABCD. Gọi K và L là hai điểm thuộc BC sao cho BK = KL = LC. Tính tỉ số diện tích của: Tam giác DAc và tứ giác ADLB

Xem đáp án

Ta có: $S_{A D L B}$ = $S_{A D B}$ + $S_{D L B}$

$∆$ DBC và $∆$ DLB có chung chiều cao kẻ từ D, Cạnh đáy LB = 2/3 BC ⇒ $S_{D L B}$ = 2/3 $S_{D B C}$

Mà $S_{D A C}$ = $S_{A D B}$ = $S_{D B C}$ (chứng minh trên)

Suy ra: $S_{A D L B}$ = $S_{D A C}$ + 2/3 $S_{D A C}$ = 5/3 $S_{D A C}$ ⇒

Câu 8:

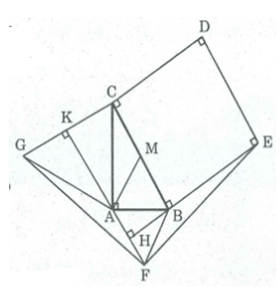
Cho tam giác ABC vuông tại A và có BC = 2AB, AB = a. Ở phía ngoài tam giác, ta vẽ hình vuông BCDE, tam giác đều ABF và tam giác đều AGC. Tính các góc B, C, cạnh AC và diện tích tam giác ABC.

Xem đáp án

Gọi M là trung điểm của BC, ta có:

AM = MB = 1/2 BC = a (tính chất tam giác vuông)

Suy ra MA = MB = AB = a

Suy ra $∆$ AMB đều ⇒ $∠$ (ABC) = $60^{0}$

Mặt khác: $∠$ (ABC) + $∠$ (ACB) = $90^{0}$ (tính chất tam giác vuông)

Suy ra: $∠$ (ACB) = $90^{0}$ - $∠$ (ABC) = $90^{0}$ – $60^{0}$ = $30^{0}$

Trong tam giác vuông ABC, theo Pi-ta-go, ta có: $B C^{2} = A B^{2} + A C^{2}$

⇒ $A C^{2} = B C^{2} - A B^{2} = 4 a^{2} - a^{2} = 3 a^{2}$ ⇒ AC = a $\sqrt{3}$

Vậy $S_{A B C}$ = 1/2 .AB.AC

= $\frac{1}{2} a . a \sqrt{3} = \frac{a^{2} \sqrt{3}}{2} (đ v d t)$

Câu 9:

Cho tam giác ABC vuông tại A và có BC = 2AB, AB = a. Ở phía ngoài tam giác, ta vẽ hình vuông BCDE, tam giác đều ABF và tam giác đều AGC. Chứng minh rằng FA vuông góc với BE và CG. Tính diện tích các tam giác FAG và FBE.

Xem đáp án

Ta có: $∠$ (FAB) = $∠$ (ABC) = $60^{0}$

FA // BC (vì có cặp góc ở vị trí so le trong bằng nhau)

BC ⊥ BE (vì BCDE là hình vuông)

Suy ra: FA ⊥ BE

BC ⊥ CD (vì BCDE là hình vuông)

Suy ra: FA ⊥ CD

Gọi giao điểm BE và FA là H, FA và CG là K.

⇒ BH ⊥ FA và FH = HA = a/2 (tính chất tam giác đều)

$∠$ (ACG) + $∠$ (ACB) + $∠$ (BCD) = $60^{0} + 30^{0} + 90^{0} = 180^{0}$

⇒ G, C, D thẳng hàng

⇒ AK ⊥ CG và GK = KC = 1/2 GC = 1/2 AC = (a $\sqrt{3}$ )/2

$S_{F A G}$ = 1/2 GK.AF =

$S_{F B E}$ = 1/2 FH.BE = 1/2 .a/2 .2a = 1/2 $a^{2}$ (đvdt)

Câu 10:

Cho tam giác ABC vuông tại A và có BC = 2AB, AB = a. Ở phía ngoài tam giác, ta vẽ hình vuông BCDE, tam giác đều ABF và tam giác đều AGC. Tính diện tích tứ giác DEFG

Xem đáp án

$S_{B C D E} = B C^{2} = {(2 a)}^{2} = 4 a^{2}$ (dvdt)

Trong tam giác vuông BHA, theo Pi-ta-go, ta có: $A H^{2} + B H^{2} = A B^{2}$

⇒ $B H^{2} = A B^{2} - A H^{2} = a^{2} - a^{2} / 4 = 3 a^{2} / 4$ ⇒ BH = (a $\sqrt{3}$ )/2

$S_{A B F}$ = 1/2 BH.FA =

Trong tam giác vuông AKG, theo Pi-ta-go, ta có: $A C^{2} = A K^{2} + K C^{2}$

⇒ $A K^{2} = A C^{2} - K C^{2} = 3 a^{2} - 3 a^{2} / 4 = 9 a^{2} / 4$ ⇒ AK = 3a/2 (đvdt)

$S_{A C G}$ = 1/2 AK.CG =

$S_{D E F G}$ = $S_{B C D E}$ + $S_{F B E}$ + $S_{FAB}$ + $S_{F A G}$ + $S_{A C G}$ + $S_{A B C}$

Câu 11:

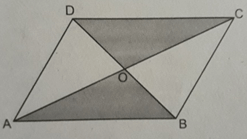
Cho hình bình hành ABCD, hai đường chéo AC và BD cắt nhau tại O. Xét các tam giác có đỉnh lấy trong số các điểm A, B, C, O, hãy chỉ ra các tam giác có diện tích bằng nhau và giải thích vì sao.

Xem đáp án

Xem hình bs.52.

- Các tam giác ADB, ACB, DAC, DBC có diện tích bằng nhau vì cùng bằng nửa diện tích hình bình hành đã cho.

- Các tam giác OAD, OCB, ODC, OBA có diện tích bằng nhau vì cùng bằng một phần tư diện tích hình bình hành đã cho.

Câu 12:

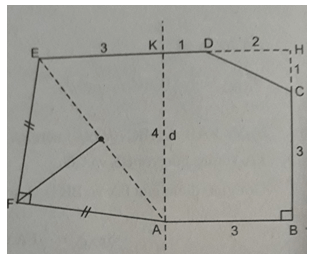
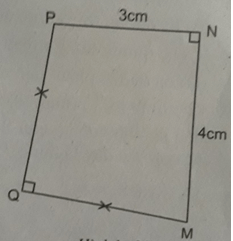
Cho hình lục giác ABCDEF, có AB = BC = 3cm và ED = 4cm. Biết rằng ED song song với AB, AB vuông góc với BC, FE vuông góc với FA vuông góc với FA và FE = FA. Qua điểm A kẻ đường thẳng d song song với BC. Gọi K là giao điểm của d và ED, biết AK = 4cm, KD = 1cm. Tính diện tích của lục giác đó.

Mỗi bài từ số II.3 đến II.11 sau đây đều có bốn phương án lựa chọn là (A), (B), (C) và (D) nhưng chỉ có một trong số đó là đúng. Hãy chỉ ra phương án mà em cho là đúng.

Xem đáp án

Gọi H là giao điểm của hai đường thẳng ED và BC. Khi đó, ABHE là hình thang và tính được diện tích của nó là

$S_{1}$ = 1/2 (AB + EH).BH = 1/2 (3 + 6).4 = 18( $c m^{2}$ ).

Diện tích của tam giác vuông DHC là

$S_{2}$ = 1/2 DH.CH = 1/2.2.1 = 1( $c m^{2}$ ).

Trong tam giác vuông AKE tính được EA = 5 (cm).

Trong tam giác vuông FEA có FE = FA suy ra $E F^{2}$ = 25/2.

Từ đó diện tích của tam giác FAE là $S_{3}$ = 25/4 $c m^{2}$

Vậy diện tích của lục giác đã cho là

S = $S_{3}$ + $S_{1}$ - $S_{2}$ = 25/4 + 18 – 1 = 93/4( $c m^{2}$ ).

Câu 13:

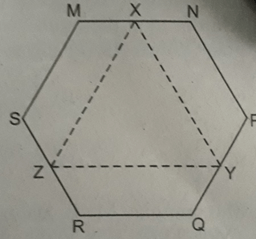
Cho lục giác đều MNPQRS (h.bs.27). Gọi X, Y, Z tương ứng là trung điểm của các cạnh MN, PQ và RS. Khi đó XYZ là:

(A) tam giác vuông;

(B) tam giác vuông cân;

(D) tam giác mà độ dài các cạnh của nó đôi một khác nhau.

Xem đáp án

Chọn C

Câu 14:

Cho tứ giác MNPQ và các kích thước đã cho trên hình bs.28. Diện tích tam giác MQP bằng bao nhiêu ( $c m^{2}$ )?

(A) 6;

(B) 25;

(D) 25/4.

Xem đáp án

Chọn D

Câu 15:

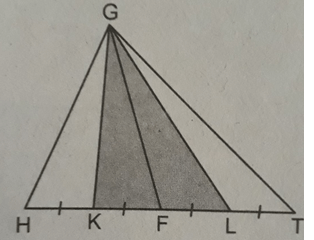
Cho hình bs.29, trong đó HK = KF = FL = LT và tam giác GHT có diện tích S. Khi đó, diện tích của tam giác GKL bằng:

(A) 1/2 S;

(B) 1/4 S;

(D) 3/4 S.

Xem đáp án

Chọn A

Câu 16:

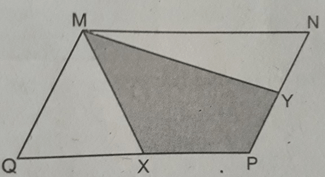
Cho hình bs.30 (hình bình hành MNPQ có diện tích S và X, Y tương ứng là trung điểm của các cạnh QP, PN). Khi đó, diện tích của tứ giác MXPY bằng:

(A) 1/4 S;

(B) 1/2 S;

(D) 3/4 S.

Xem đáp án

Chọn B

Câu 17:

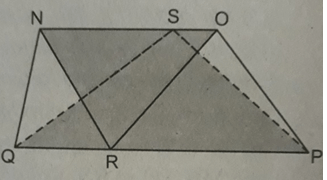
Cho hình bs.31, (R là điểm bất kì trên QS, S là điểm bất kì trên NO, hình thang NOPQ có diện tích S). Khi đó, tổng diện tích của hai tam giác QSP và NRO bằng:

(A) 1/2 S; (B) 1/4 S;

Xem đáp án

Chọn D

Câu 18:

Cho tam giác MNP. Điểm T nằm trong tam giác MNP sao cho các tam giác TMN, TMP, TPN có diện tích bằng nhau. Khi đó, T là giao điểm

(A) ba đường cao của tam giác đó;

(B) ba đường trung trực của tam giác đó;

(D) ba đường phân giác trong của tam giác đó.

Xem đáp án

Chọn C

Câu 19:

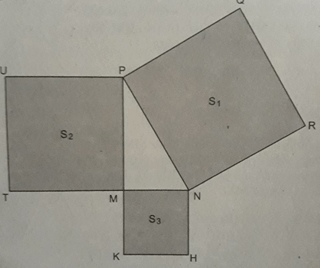
Cho hình bs.32 (tam giác MNP vuông tại đỉnh M và NRQP, PUTM, MKHN đều là hình vuông, còn $S_{1}, S_{2}, S_{3}$ tương ứng là diện tích của một hình). Quan hệ nào sau đây là đúng?