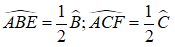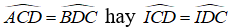18 câu hỏi trắc nghiệm thuộc Bài 3: Toán 8 Hình thang cân

Giải Sách Bài Tập Toán 8 Tập 1

Đề số 1
Đề số 2
Đề số 3
Đề số 4
Đề số 5
Đề số 6
Đề số 7
Đề số 8
Đề số 9
Đề số 10
Đề số 11
Đề số 12
Đề số 13
Đề số 14
Đề số 15
Đề số 16
Đề số 17
Đề số 18
Đề số 19
Đề số 20
Đề số 21
Đề số 22
Đề số 23
Đề số 24
Đề số 25
Đề số 26
Đề số 27
Đề số 28
Đề số 29
Đề số 30
Đề số 31
Đề số 32
Đề số 33
Đề số 34
Đề số 35
Đề số 36
Đề số 37
Đề số 38
Đề số 39
Đề số 40
Đề số 41

Bài 3: Toán 8 Hình thang cân

7180 lượt thi
18 câu hỏi
30 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

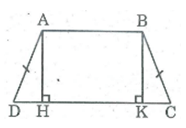
Hình thang cân ABCD có AB //CD, AB < CD. Kẻ các đường cao AH, BK. Chứng minh rằng: DH = CK

Xem đáp án

Xét hai tam giác vuông AHD và BKC:

$∠$ (AHD) = $∠$ (BKC) = $90^{0}$

AD = BC (tính chất hình thang cân)

$∠$ C = $∠$ D (gt)

Suy ra: $∆$ AHD = $∆$ BKC (cạnh huyền, góc nhọn)

⇒ HD = KC

Câu 2:

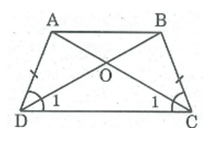
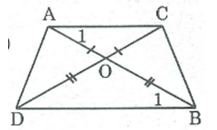
Hình thang cân ABCD có AB // CD, O là giao điểm của hai đường chéo. Chứng minh rằng OA = OB, OC = OD.

Xem đáp án

Xét $∆$ ADC và $∆$ BCD, ta có:

AD = BC (tính chất hình thang cân)

$∠$ (ADC) = $∠$ (BCD) (gt)

DC chung

Do đó: $∆$ ADC = $∆$ BCD (c.g.c) ⇒ $∠ C_{1}$ = $∠ D_{1}$

Trong $∆$ OCD ta có: $∠ C_{1}$ = $∠ D_{1}$ ⇒ $∆$ OCD cân tại O ⇒ OC = OD (1)

AC = BD (tính chất hình thang cân) ⇒ AO + OC = BO + OD (2)

Từ (1) và (2) suy ra: AO = BO.

Câu 3:

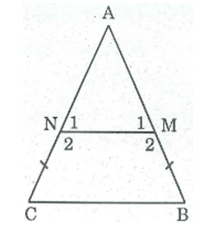
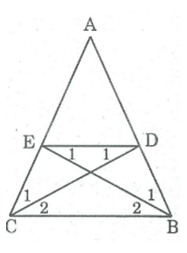
Cho tam giác ABC cân tại A. Trên cạnh AB, AC lấy các điểm M, N sao cho BM = CN. Tứ giác BMNC là hình gì? Vì sao?

Xem đáp án

$∆$ ABC cân tại A

⇒ $∠$ B = $∠$ C = ( $180^{0}$ - $∠$ A) / 2 (tính chất tam giác cân) (1)

AB = AC (gt) ⇒ AM + BM = AN + CN

Mà BM = CN (gt) ⇒ AM = AN

⇒ $∆$ AMN cân tại A

⇒ $∠ M_{1}$ = $∠ N_{1}$ = ( $180^{0}$ - $∠$ A) / 2 (tính chất tam giác cân) (2)

Từ (1) và (2) suy ra: $∠ M_{1}$ = $∠$ B

⇒ MN // BC (vì có cặp góc đồng vị bằng nhau)

Tứ giác BCNM là hình thang có $∠$ B = $∠$ C

Vậy BCNM là hình thang cân.

Câu 4:

Cho tam giác ABC cân tại A. Trên cạnh AB, AC lấy các điểm M, N sao cho BM = CN. Tính các góc của tứ giác BMNC biết rang góc $∠$ A = $40^{0}$

Xem đáp án

$∠$ B = $∠$ C = ( $180^{0}$ – $40^{0}$ ) / 2 = $70^{0}$

Mà $∠ M_{2}$ + $∠$ B = $180^{0}$ (hai góc trong cùng phía nên bù nhau)

Suy ra: $∠ M_{2}$ = $180^{0}$ - $∠$ B = $180^{0}$ – $70^{0}$ = $110^{0}$

$∠ N_{2}$ = $∠ M_{2}$ = $110^{0}$ (tính chất hình thang cân)

Câu 5:

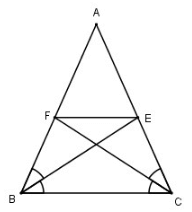
Cho tam giác ABC cân tại A, các đường phân giác BE, CF. Chứng minh rằng BFEC là hình thang cân có đáy nhỏ bằng cạnh bên.

Xem đáp án

+) Do BE và CF lần lượt là tia phân giác của góc B và góc C nên ta có:

Mà tam giác ABC cân tại A nên $∠$ B = $∠$ C

Suy ra: $∠$ ABE = $∠$ ACF

Xét hai tam giác AEB và AFC

Có AB = AC ( $∆$ ABC cân tại A)

$∠$ ABE = $∠$ ACF (chứng minh trên)

$∠$ A là góc chung

⇒ $∆$ AEB = $∆$ AFC (g.c.g) ⇒ AE = AF ⇒ $∆$ AEF cân tại A

⇒ $∠$ AFE = ( $180^{0}$ − $∠$ A) / 2 và trong tam giác $∆$ ABC: $∠$ B = ( $180^{0}$ − ∠A) / 2

⇒ $∠$ AFE = $∠$ B ⇒ FE//BC ( có hai góc ở vị trí đồng vị bằng nhau).

⇒ Tứ giác BFEC là hình thang.

Vì FE//BC nên ta có: $∠$ FEB = $∠$ EBC (so le trong)

Lại có: $∠$ FBE = $∠$ EBC ( vì BE là tia phân giác của góc B)

⇒ $∠$ FBE = $∠$ FEB

⇒ $∆$ FBE cân ở F ⇒ FB = FE

⇒ Hình thang BFEC là hình thang cân có đáy nhỏ bằng cạnh bên (đpcm)

Câu 6:

Chứng minh hình thang có hai đường chéo bằng nhau là hình thang cân.

Xem đáp án

Từ B kẻ đường thẳng song song với AC cắt đường thẳng DC tại K.

Ta có hình thang ABKC có hai cạnh bên BK // AC nên AC = BK

Mà AC = BD (gt)

Suy ra: BD = BK do đó $∆$ BDK cân tại B

⇒ $∠ D_{1}$ = $∠$ K (tính chất hai tam giác cân)

Ta lại có: $∠ C_{1}$ = $∠$ K (hai góc đồng vị)

Suy ra: $∠ D_{1}$ = $∠ C_{1}$

Xét $∆$ ACD và $∆$ BDC:

AC = BD (gt)

$∠ C_{1}$ = $∠ D_{1}$ (chứng minh trên)

CD chung

Do đó $∆$ ACD = $∆$ BDC (c.g.c) ⇒ $∠$ (ADC) = $∠$ (BCD)

Hình thang ABCD có $∠$ (ADC) = $∠$ (BCD) nên là hình thang cân.

Câu 7:

Tính các góc của hình thang cân, biết một góc bằng $50^{0}$

Xem đáp án

Giả sử hình thang ABCD có AB // CD và $∠$ D = $50^{0}$

Vì $∠$ C = $∠$ D (tính chất hình thang cân)

⇒ $∠$ C = $50^{0}$

$∠$ A + $∠$ D = $180^{0}$ (hai góc trong cùng phía)

⇒ $∠$ A = $180^{0}$ - $∠$ D = $180^{0}$ – $50^{0}$ = $130^{0}$

$∠$ B = $∠$ A (tính chất hình thang cân)

Suy ra: $∠$ B = $130^{0}$

Câu 8:

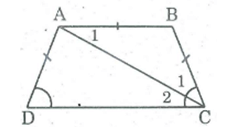
Hình thang cân ABCD có đáy nhỏ AB bằng cạnh bên AD. Chứng minh rằng CA là tia phân giác của góc C.

Xem đáp án

Ta có:

AB = AD (gt)

AD = BC (tính chất hình thang cân)

⇒ AB = BC do đó ΔABC cân tại B

⇒ $∠$ BAC = $∠$ BCA (tính chất tam giác cân) (*)

ABCD là hình thang có đáy là AB nên AB // CD

$∠$ BAC = $∠$ DCA (hai góc so le trong) (**)

Từ (*) và (**) suy ra: $∠$ BCA = $∠$ DCA (cùng bằng $∠$ BAC)

Vậy CA là tia phân giác của $∠$ BCD.

Câu 9:

Hai đoạn thẳng AB và CD cắt nhau tại 0. Biết rằng OA = OC, OB = OD. Tứ giác ABCD là hình gì ? Vì sao

Xem đáp án

Ta có: OA = OC (gt)

⇒ $∆$ OAC cân tại O

⇒ $∠ A_{1}$ = ( $180^{0}$ - $∠$ (AOC) ) / 2 (tính chất tam giác cân) (1)

OB = OD (gt)

⇒ $∆$ OBD cân tại O

⇒ $∠ B_{1}$ = ( $180^{0}$ - $∠$ (BOD) )/2 (tính chất tam giác cân) (2)

$∠$ (AOC) = $∠$ (BOD) (đối đỉnh) (3)

Từ (1), (2), (3) suy ra: $∠ A_{1}$ = $∠ B_{1}$

⇒ AC // BD (vì có cặp góc ở vị tri so le trong bằng nhau)

Suy ra: Tứ giác ACBD là hình thang

Ta có: AB = OA + OB

CD = OC + OD

Mà OA = OC, OB = OD

Suy ra: AB = CD

Vậy hình thang ABCD là hình thang cân.

Câu 10:

Cho tam giác ABC cân tại A. Lấy điểm D trên cạnh AB, điểm E trên cạnh AC sao cho AD = AE. Tứ giác BDEC là hình gì ? Vì sao

Xem đáp án

AD = AE (gt)

⇒ $∆$ ADE cân tại A ⇒ $∠$ (ADE) = ( $180^{0}$ - $∠$ A )/2

$∆$ ABC cân tại A ⇒ $∠$ (ABC) = ( $180^{0}$ - $∠$ A )/2

Suy ra: $∠$ (ADE) = $∠$ (ABC)

⇒ DE // BC (Vì có cặp góc đồng vị bằng nhau)

Tứ giác BDEC là hình thang

$∠$ (ABC) = $∠$ (ACB) (tính chất tam giác cân) hay $∠$ (DBC) = $∠$ (ECB)

Vậy BDEC là hình thang cân.

Câu 11:

Cho tam giác ABC cân tại A. Lấy điểm D trên cạnh AB, điểm E trên cạnh AC sao cho AD = AE. Các điểm D, E ở vị trí nào thì BD =DE = EC?

Xem đáp án

Ta có: BD = DE ⇒ $∆$ BDE cân tại D

$∠ B_{1}$ = $∠ E_{1}$

Mà $∠ E_{1}$ = $∠ B_{2}$ (so le trong)

⇒ $∠ B_{1}$ = $∠ B_{2}$

DE = EC ⇒ $∆$ DEC cân tại E

⇒ $∠ D_{1}$ = $∠ C_{1}$

$∠ D_{1}$ = $∠ C_{2}$ (so le trong)

⇒ $∠ C_{1}$ = $∠ C_{2}$

Vậy khi BE là tia phân giác của $∠$ (ABC) , CD là tia phân giác của $∠$ (ACB) thì BD = DE = EC

Câu 12:

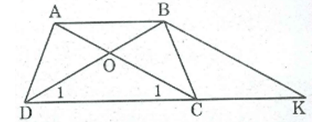
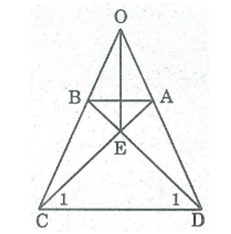
Hình thang cân ABCD có 0 là giao điểm của hai đường thắng chứa cạnh bên AD, BC và E là giao điểm của hai đường chéo. Chứng minh rằng OE là đường trung trực của hai đáy.

Xem đáp án

Ta có: $∠$ (ADC) = $∠$ (BCD) (gt)

⇒ $∠$ (ODC) = $∠$ (OCD)

⇒ $∆$ OCD cân tại O

⇒ OC = OD

OB + BC = OA + AD

Mà AD = BC (tính chất hình thang cân)

⇒ OA = OB

Xét $∆$ ADC và $∆$ BCD:

AD = BC (tính chất hình thang cân )

AC = BD (tính chất hình thang cân)

CD chung

Do đó $∆$ ADC và $∆$ BCD (c.c.c)

⇒ $∠ D_{1}$ = $∠ C_{1}$

⇒ $∆$ EDC cân tại E

⇒ EC = ED nên E thuộc đường trung trực CD

OC = OD nên O thuộc đường trung trực CD

E $\neq$ O. Vậy OE là đường trung trực của CD.

Ta có: BD= AC (tính chất hình thang cân)

⇒ EB + ED = EA + EC mà ED = EC

⇒ EB = EA nên E thuộc đường trung trực AB

OA = OB (chứng minh trên ) nên O thuộc đường trung trực của AB

E $\neq$ O. Vậy OE là đường trung trực của AB.

Câu 13:

Hình thang ABCD có đáy nhỏ AB = b , đáy lớn CD = a, đường cao AH. Chứng minh rằng HD = (a - b) / 2 , HC = (a + b) / 2 (a, b có cùng đơn vị đo).

Xem đáp án

Kẻ đường cao BK

Xét hai tam giác vuông AHD và BKC, ta có:

$∠$ (AHD) = $∠$ (BKC) = $90^{0}$

AD = BC (tỉnh chất hình thang-Cân)

$∠$ D = $∠$ C (gt)

Do đó: $∆$ AHD = $∆$ BKC (cạnh huyền, góc nhọn) ⇒ HD = KC.

Hình thang ABKH có hai cạnh bên song song nên AB = HK

a – b = DC – AB = DC – HK = HD + KC = 2HD ⇒ HD = (a – b) / 2

HC = DC – HD = a - (a – b) / 2 = (a + b) / 2

Câu 14:

Tính đường cao của hình thang cân có hai đáy 10cm, 26cm và cạnh bên 17cm

Xem đáp án

HD = (CD – AB) / 2 = (26 – 10) / 2 = 8 (cm)

Trong tam giác vuông AHD có $∠$ (AHD) = $90^{0}$

$A D^{2} = A H^{2} + H D^{2}$ (định lý Pi-ta-go)

⇒ $A H^{2} = A D^{2} - H D^{2}$

$A H^{2} = 17^{2} - 8^{2}$ = 289 – 64 = 225

AH = 15 (cm)

Câu 15:

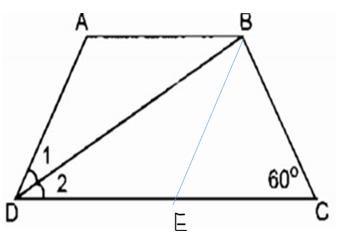
Hình thang cân ABCD có đường chéo BD vuông góc với cạnh bên BC, BD là tia phân giác của-góc D. Tính chu vi của hình thang, biết BC = 3cm.

Xem đáp án

Ta có: AD = BC = 3 (cm) (tính chất hình thang cân)

$∠$ (ABD) = $∠$ (BDC) (so le trong)

$∠$ (ADB) = $∠$ (BDC) ( do DB là tia phân giác của góc D )

⇒ $∠$ (ABD) = $∠$ (ADB)

⇒ $∆$ ABD cân tại A

⇒ AB = AD = 3 (cm)

$∆$ BDC vuông tại B

$∠$ (BDC) + $∠$ C = $90^{0}$

$∠$ (ADC) = $∠$ C (gt)

Mà $∠$ (BDC) = 1/2 $∠$ (ADC) nên $∠$ (BDC) = 1/2 $∠$ C

$∠$ C + 1/2 $∠$ C = $90^{0}$ ⇒ $∠$ C = $60^{0}$

Từ B kẻ đường thẳng song song AD cắt CD tại E.

Hình thang ABED có hai cạnh bên song song nên AB = DE và AD = BE

⇒ DE = 3 (cm), BE = 3 (cm)

$∠$ (BEC) = $∠$ (ADC) (đồng vị)

Suy ra: $∠$ (BEC) = $∠$ C

⇒ $∆$ BEC cân tại B có $∠$ C = $60^{0}$

⇒ $∆$ BEC đều

⇒ EC = BC = 3 (cm)

CD = CE + ED = 3 + 3 = 6(cm)

Chu vi hình thang ABCD bằng:

AB + BC + CD + DA = 3 + 3 + 6 + 3 = 15 (cm)

Câu 16:

Hình thang cân ABCD (AB// CD) có $∠$ (A ) = $70^{0}$ . Khẳng định nào dưới đây là đúng ?

A. $∠$ (C ) = $110^{0}$

B. $∠$ (B ) = $110^{0}$

C. $∠$ (C ) = $70^{0}$

D. $∠$ (D ) = $70^{0}$

Xem đáp án

Chọn A. $∠$ (C ) = $110^{0}$

Ta có : $∠$ (A )+ $∠$ (D )= $180^{0}$ ( hai góc trong cùng phía)

=> $∠$ (D )= $180^{0}$ - $∠$ (A )= $180^{0}$ - $70^{0}$ = $110^{0}$

mà $∠$ (C )= $∠$ (D ) (tính chất hình thang cân ) => $∠$ (C )= $∠$ (D )= $110^{0}$

Câu 17:

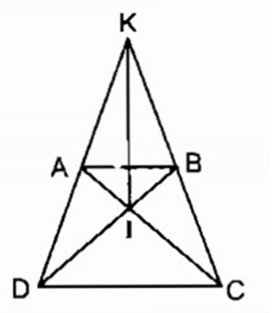
Hình thang cân ABCD (AB// CD) có hai đường chéo cắt nhau tại I, hai đường thẳng chứa các cạnh bên cắt nhau ở K. Chứng minh rằng KI là đường trung trực của hai đáy.

Xem đáp án

$∆$ ACD = $∆$ BDC (c.c.c)

Suy ra

⇒ Tam giác ICD cân tại I.

do đó ID = IC (1)

Tam giác KCD có hai góc ở đáy bằng nhau $∠$ C = $∠$ D nên tam giác KCD cân tại K

⇒ KD = KC (2)

Từ (1) và (2) suy ra KI là đường trung trực của CD.

Chứng minh tương tự có IA = IB, KA = KB

Suy ra KI là đường trung trực của AB

Câu 18:

Hình thang cân ABCD (AB // CD) có , DB là tia phân giác của góc D. Tính các cạnh của hình thang, biết chu vi hình thang bằng 20cm.

Xem đáp án

Hình thang ABCD cân có AB // CD

⇒ $∠$ D = $∠$ C = $60^{0}$

DB là tia phân giác của góc D

⇒ $∠$ (ADB) = $∠$ (BDC)

$∠$ (ABD) = $∠$ (BDC) (hai góc so le trong)

Suy ra: $∠$ (ADB) = $∠$ (ABD)

⇒ $∆$ ABD cân tại A ⇒ AB = AD (1)

Từ B kẻ đường thẳng song song với AD cắt CD tại E

Hình thang ABED có hai cạnh bên song song nên AB = ED, AD= BE (2)

$∠$ (BEC) = $∠$ (ADC) (đồng vị )

Suy ra: $∠$ (BEC) = $∠$ C = $60^{0}$

⇒ $∆$ BEC đều ⇒ EC = BC (3)

AD = BC (tính chất hình thang cân) (4)

Từ (1), (2), (3) và (4) ⇒ AB = BC = AD = ED = EC

⇒ Chu vi hình thang bằng:

AB + BC + CD + AD = AB + BC + EC + ED + AD = 5AB

⇒AB = BC = AD = 20 : 5 = 4 (cm)

CD = CE + DE = 2 AB = 2.4 = 8 (cm)

Bắt đầu thi ngay

CHỌN BỘ SÁCH BẠN MUỐN XEM

Giải Sách Bài Tập Toán 8 Tập 1

Bài 3: Toán 8 Hình thang cân

Danh sách câu hỏi

Bài thi liên quan