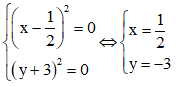33 câu hỏi trắc nghiệm thuộc Bài 3, 4, 5: Những hằng đẳng thức đáng nhớ

Giải Sách Bài Tập Toán 8 Tập 1

Đề số 1
Đề số 2
Đề số 3
Đề số 4
Đề số 5
Đề số 6
Đề số 7
Đề số 8
Đề số 9
Đề số 10
Đề số 11
Đề số 12
Đề số 13
Đề số 14
Đề số 15
Đề số 16
Đề số 17
Đề số 18
Đề số 19
Đề số 20
Đề số 21
Đề số 22
Đề số 23
Đề số 24
Đề số 25
Đề số 26
Đề số 27
Đề số 28
Đề số 29
Đề số 30
Đề số 31
Đề số 32
Đề số 33
Đề số 34
Đề số 35
Đề số 36
Đề số 37
Đề số 38
Đề số 39
Đề số 40
Đề số 41

Bài 3, 4, 5: Những hằng đẳng thức đáng nhớ

7196 lượt thi
33 câu hỏi
30 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

Tính: ${(x + 2 y)}^{2}$

Xem đáp án

${(x + 2 y)}^{2}$ = $x^{2}$ +2.x.2y + ${(2 y)}^{2}$

= $x^{2}$ + 4xy + 4 $y^{2}$

Câu 2:

Tính: (x – 3y)(x + 3y)

Xem đáp án

(x – 3y)(x + 3y) = $x^{2}$ – ${(3 y)}^{2}$ = $x^{2}$ – 9 $y^{2}$

Câu 3:

Tính: ${(5 - x)}^{2}$

Xem đáp án

${(5 - x)}^{2}$ = $5^{2}$ – 2.5x + $x^{2}$ = 25 – 10x + $x^{2}$

Câu 4:

Tính: ${(x - 1)}^{2}$

Xem đáp án

${(x - 1)}^{2}$ = $x^{2}$ – 2.x.1 + $1^{2}$ = $x^{2}$ –2x + 1

Câu 5:

Tính: ${(3 - y)}^{2}$

Xem đáp án

${(3 - y)}^{2}$ = $3^{2}$ – 2.3.y + $y^{2}$ = 9 – 6y + $y^{2}$

Câu 6:

Tính: ${(x - 1 / 2)}^{2}$

Xem đáp án

${(x - 1 / 2)}^{2}$ = $x^{2}$ - 2.x.1/2 + ${(1 / 2)}^{2}$ = $x^{2}$ – x + 1/4

Câu 7:

Viết các biểu thức sau dưới dạng bình phương một tổng: $x^{2}$ + 6x + 9

Xem đáp án

$x^{2}$ + 6x + 9 = $x^{2}$ + 2.x.3 + $3^{2}$ = ${(x + 3)}^{2}$

Câu 8:

Viết các biểu thức sau dưới dạng bình phương một tổng: $x^{2}$ + x + 1/4

Xem đáp án

$x^{2}$ + x + 1/4 = $x^{2}$ + 2.x.1/2 + ${(1 / 2)}^{2}$ = ${(x + 1 / 2)}^{2}$

Câu 9:

Viết các biểu thức sau dưới dạng bình phương một tổng: 2x $y^{2}$ + $x^{2}$ $y^{4}$ + 1

Xem đáp án

2x $y^{2}$ + $x^{2}$ $y^{4}$ + 1 = ${(x y^{2})}^{2}$ + 2.x $y^{2}$ .1 + $1^{2}$ = ${(x y^{2} + 1)}^{2}$

Câu 10:

Rút gọn biểu thức: (x + y)2 + (x – y)2

Xem đáp án

${(x + y)}^{2} + {(x - y)}^{2}$

= $x^{2}$ + 2xy + $y^{2}$ + $x^{2}$ – 2xy + $y^{2}$

= 2 $x^{2}$ + 2 $y^{2}$

Câu 11:

Rút gọn biểu thức: 2(x – y)(x + y) + ${(x + y)}^{2}$ + ${(x - y)}^{2}$

Xem đáp án

2(x – y)(x + y) + ${(x + y)}^{2}$ + ${(x - y)}^{2}$

= ${(x + y)}^{2}$ +2( x+ y).(x- y) + ${(x - y)}^{2}$

(áp dụng hằng đẳng thức thứ 1với A = x+ y, B = x- y)

= ${[(x + y) + (x - y)]}^{2} = {(2 x)}^{2} = 4 x^{2}$

Câu 12:

Rút gọn biểu thức: ${(x - y + z)}^{2}$ + ${(z - y)}^{2}$ + 2(x – y + z)(y – z)

Xem đáp án

${(x - y + z)}^{2}$ + ${(z - y)}^{2}$ + 2(x – y + z)(y – z)

= ${(x - y + z)}^{2}$ + 2(x – y + z)(y – z) + ${(y - z)}^{2}$

= ${[(x - y + z) + (y - z)]}^{2} = x^{2}$

Câu 13:

Biết số tự nhiên a chia cho 5 dư 4. Chứng minh rằng $a^{2}$ chia cho 5 dư 1.

Xem đáp án

Số tự nhiên a chia cho 5 dư 4, ta có: a = 5k + 4 (k ∈N)

Ta có: $a^{2}$ = ${(5 k + 4)}^{2}$

= 25 $k^{2}$ + 40k + 16

= 25 $k^{2}$ + 40k + 15 + 1

= 5(5 $k^{2}$ + 8k +3) +1

Ta có: 5 ⋮ 5 nên 5(5 $k^{2}$ + 8k + 3) ⋮ 5

Vậy $a^{2}$ = ${(5 k + 4)}^{2}$ chia cho 5 dư 1. (đpcm)

Câu 14:

Tính giá trị của biểu thức sau: $x^{2}$ – $y^{2}$ tại x = 87 và y = 13

Xem đáp án

Ta có: $x^{2}$ – $y^{2}$ = (x + y)(x – y)

Thay x = 87, y = 13, ta được:

$x^{2}$ – $y^{2}$ = (x + y)(x – y)

= (87 + 13)(87 – 13)

= 100.74 = 7400

Câu 15:

Tính giá trị của biểu thức sau: $x^{3}$ – 3 $x^{2}$ + 3x – 1 tại x = 101

Xem đáp án

$x^{3}$ - 3 $x^{2}$ + 3x - 1 tại x = 101.

= $x^{3}$ - 3. $x^{2}$ .1 + 3.x. $1^{2}$ - $1^{3}$ = ${(x - 1)}^{3}$

= ${(101 - 1)}^{3} = 100^{3}$ = 1000000

Câu 16:

Tính giá trị của biểu thức sau: $x^{3}$ + 9 $x^{2}$ + 27x + 27 tại x = 97

Xem đáp án

Ta có: $x^{3}$ + 9 $x^{2}$ + 27x + 27

= $x^{3}$ + 3. $x^{2}$ .3 + 3.x. $3^{2}$ + $3^{3}$

= ${(x + 3)}^{3}$

Thay x = 97, ta được: ${(x + 3)}^{3}$ = ${(97 + 3)}^{3}$ = $100^{3}$ = 1000000

Câu 17:

Chứng minh rằng: (a + b)( $a^{2}$ – ab + $b^{2}$ ) + (a – b)( $a^{2}$ + ab + $b^{2}$ ) = 2 $a^{3}$

Xem đáp án

Biến đổi vế trái ta có:

VT = (a + b)( $a^{2}$ – ab + $b^{2}$ ) + (a – b)( $a^{2}$ + ab + $b^{2}$ )

= $a^{3}$ + $b^{3}$ + $a^{3}$ – $b^{3}$ = 2 $a^{3}$ = VP

Vế trái bằng vế phải nên đẳng thức được chứng minh.

Câu 18:

Chứng minh rằng: $a^{3}$ + $b^{3}$ = (a + b)[ ${(a - b)}^{2}$ + ab]

Xem đáp án

Biến đổi vế trái ta có:

VT = $a^{3}$ + $b^{3}$ =(a+b)( $a^{2}$ -ab+ $b^{2}$ )

=(a+b)( $a^{2}$ -2ab+ $b^{2}$ +ab)

=(a + b)[ ${(a - b)}^{2}$ + ab] = VP

Vế phải bằng vế trái nên đẳng thức được chứng minh.

Câu 19:

Chứng minh rằng: ( $a^{2}$ + $b^{2}$ )( $c^{2}$ + $d^{2}$ ) = ${(a c + b d)}^{2} + {(a d - b c)}^{2}$

Xem đáp án

Biến đổi vế trái ta có:

VT = ( $a^{2}$ + $b^{2}$ )( $c^{2}$ + $d^{2}$ )

= $a^{2}$ $c^{2}$ + $a^{2}$ $d^{2}$ + $b^{2}$ $c^{2}$ + $b^{2}$ $d^{2}$

= ( $a^{2}$ $c^{2}$ + 2abcd + $b^{2}$ $d^{2}$ ) + ( $a^{2}$ d2 – 2abcd + $b^{2}$ $c^{2}$ )

= ${(a c + b d)}^{2} + {(a d - b c)}^{2}$ =VP

Vế phải bằng vế trái nên đẳng thức được chứng minh.

Câu 20:

Chứng tỏ rằng: $x^{2}$ – 6x + 10 > 0 với mọi x

Xem đáp án

Ta có: $x^{2}$ – 6x + 10 = $x^{2}$ – 2.x.3 + 9 + 1 = ${(x - 3)}^{2}$ + 1

Vì ${(x - 3)}^{2}$ ≥ 0 với mọi x nên ${(x - 3)}^{2}$ + 1 > 0 mọi x

Vậy $x^{2}$ – 6x + 10 > 0 với mọi x.(đpcm)

Câu 21:

Chứng tỏ rằng: 4x – $x^{2}$ – 5 < 0 với mọi x

Xem đáp án

Ta có: 4x – $x^{2}$ – 5 = -( $x^{2}$ – 4x + 4) – 1 = - ${(x - 2)}^{2}$ -1

Vì ${(x - 2)}^{2}$ ≥ 0 với mọi x nên – ${(x - 2)}^{2}$ ≤ 0 với mọi x.

Suy ra: - ${(x - 2)}^{2}$ -1 ≤ -1 với mọi x

Vậy 4x – $x^{2}$ – 5 < 0 với mọi x.(đpcm)

Câu 22:

Tìm giá trị nhỏ nhất của các đa thức: P = $x^{2}$ – 2x + 5

Xem đáp án

Ta có: P = $x^{2}$ – 2x + 5 = $x^{2}$ – 2x + 1 + 4 = ${(x - 1)}^{2}$ + 4

Vì ${(x - 1)}^{2}$ ≥ 0 nên ${(x - 1)}^{2}$ + 4 ≥ 4

Suy ra: P = 4 là giá trị bé nhất khi ${(x - 1)}^{2}$ = 0 ⇒ x = 1

Vậy P = 4 là giá trị bé nhất của đa thức khi x = 1.

Câu 23:

Tìm giá trị nhỏ nhất của các đa thức: Q = 2 $x^{2}$ – 6x

Xem đáp án

Ta có: Q = 2 $x^{2}$ – 6x = 2( $x^{2}$ – 3x) = 2( $x^{2}$ – 2.3/2 x + 9/4 - 9/4)

= 2[ ${(x - 3 / 2)}^{2}$ - 9/4 ] = 2 ${(x - 3 / 2)}^{2}$ - 9/2

Vì ${(x - 3 / 2)}^{2}$ ≥ 0 nên 2 ${(x - 3 / 2)}^{2}$ ≥ 0 ⇒ 2 ${(x - 3 / 2)}^{2}$ - 9/2 ≥ - 9/2

Suy ra: Q = - 9/2 là giá trị nhỏ nhất khi ${(x - 3 / 2)}^{2}$ = 0 ⇒ x = 3/2

Vậy Q = - 9/2 là giá trị nhỏ nhất của đa thức khi x = 3/2.

Câu 24:

Tìm giá trị nhỏ nhất của các đa thức: M = $x^{2}$ + $y^{2}$ – x + 6y + 10

Xem đáp án

Ta có: M = $x^{2}$ + $y^{2}$ – x + 6y + 10 = ( $y^{2}$ + 6y + 9) + ( $x^{2}$ – x + 1)

= ${(y + 3)}^{2}$ + ( $x^{2}$ – 2.1/2 x + 1/4) + 3/4 = ${(y + 3)}^{2}$ + ${(x - 1 / 2)}^{2}$ + 3/4

Vì ${(y + 3)}^{2}$ ≥ 0 và ${(x - 1 / 2)}^{2}$ ≥ 0 nên ${(y + 3)}^{2}$ + ${(x - 1 / 2)}^{2}$ ≥ 0

⇒ M = ${(y + 3)}^{2}$ + ${(x - 1 / 2)}^{2}$ + 3/4 ≥ 3/4

⇒ M = 3/4 khi

Vậy M = 3/4 là giá trị nhỏ nhất tại y = -3 và x = 1/2

Câu 25:

Tìm giá trị lớn nhất của đa thức: A = 4x – $x^{2}$ + 3

Xem đáp án

Ta có: A = 4x – $x^{2}$ + 3

= 7 – $x^{2}$ + 4x – 4

= 7 – ( $x^{2}$ – 4x + 4)

= 7 – ${(x - 2)}^{2}$

Vì ${(x - 2)}^{2}$ ≥ 0 với mọi x nên A = 7 – ${(x - 2)}^{2}$ ≤ 7

Vậy giá trị của A lớn nhất là 7 khi x – 2 = 0 hay x = 2

Câu 26:

Tìm giá trị lớn nhất của đa thức: B = x – $x^{2}$

Xem đáp án

Ta có: B = x – $x^{2}$

= 1/4 - $x^{2}$ + x - 1/4

= 1/4 - ( $x^{2}$ - 2.x. 1/2 + 1/4 )

= 1/4 - ${(x - 1 / 2)}^{2}$

Vì ${(x - 1 / 2)}^{2}$ ≥ 0 với mọi x nên B = 1/4 - ${(x - 1 / 2)}^{2}$ ≤ 1/4

Vậy giá trị lớn nhất của B là 1/4 khi x- 1/2 = 0 hay x = 1/2 .

Câu 27:

Tìm giá trị lớn nhất của đa thức: N = 2x – 2 $x^{2}$ – 5

Xem đáp án

Ta có: N = 2x – 2 $x^{2}$ – 5

= - 2( $x^{2}$ – x + 5/2 )

= - 2( $x^{2}$ – 2.x. 1/2 + 1/4 + 9/4 )

= - 2[ ${(x - 1 / 2)}^{2}$ + 9/4 ]

= - 2 ${(x - 1 / 2)}^{2}$ - 9/2

Vì ${(x - 1 / 2)}^{2}$ ≥ 0 với mọi x nên - 2 ${(x - 1 / 2)}^{2}$ ≤ 0

Suy ra: N = - 2 ${(x - 1 / 2)}^{2}$ - 9/2 ≤ - 9/2

Vậy giá trị lớn nhất của biểu thức N là - 9/2 khi x- ½ = 0 hay x = 1/2 .

Câu 28:

Cho $x^{2}$ + $y^{2}$ = 26 và xy = 5, giá trị của ${(x - y)}^{2}$ là:

A. 4

B. 16

C. 21

D. 36

Xem đáp án

Chọn B

Ta có: ${(x - y)}^{2}$ = $x^{2}$ -2xy+ $y^{2}$ = ( $x^{2}$ + $y^{2}$ ) - 2xy = 26 - 2.5=16

Câu 29:

Kết quả của tích $(a^{2} + 2 a + 4) (a - 2)$ là:

A. ${(a + 2)}^{3}$

B. ${(a - 2)}^{3}$

C. $a^{3}$ + 8

D. $a^{3}$ − 8

Xem đáp án

Chọn D.

Cách 1: $(a^{2} + 2 a + 4) (a - 2)$ = $a^{3}$ -2 $a^{2}$ +2 $a^{2}$ -4a+4a-8= $a^{3}$ – 8

Cách 2: $(a^{2} + 2 a + 4) (a - 2)$ = (a- 2).( $a^{2}$ + 2a + 4) = $a^{3}$ – 8 ( hằng đẳng thức).

Câu 30:

Rút gọn các biểu thức: P = (5x − 1) + 2(1 − 5x)(4 + 5x) + ${(5 x + 4)}^{2}$

Xem đáp án

P = (5x − 1) + 2(1 − 5x)(4 + 5x) + ${(5 x + 4)}^{2}$

= 5x – 1 + (2 – 10x).( 4+ 5x) + ${(5 x + 4)}^{2}$

= 5x – 1 + 8 + 10x – 40x – 50 $x^{2}$ + 25 $x^{2}$ + 40x + 16

= (- 50 $x^{2}$ + 25 $x^{2}$ )+ ( 5x + 10x – 40x + 40x) + (- 1+ 8 + 16)

= -25 $x^{2}$ + 15x + 23

Câu 31:

Rút gọn các biểu thức: Q = ${(x - y)}^{3}$ + ${(y + x)}^{3}$ + ${(y - x)}^{3}$ – 3xy(x + y)

Xem đáp án

Q = ${(x - y)}^{3}$ + ${(y + x)}^{3}$ + ${(y - x)}^{3}$ – 3xy(x + y)

= $x^{3}$ – 3 $x^{2}$ y + 3x $y^{2}$ – $y^{3}$ + $y^{3}$ + 3 $y^{2}$ .x + 3y $x^{2}$ + $x^{3}$ + $y^{3}$ – 3 $y^{2}$ .x +3y $x^{2}$ – $x^{3}$ – 3 $x^{2}$ y – 3x $y^{2}$

= $x^{3}$ – 3 $x^{2}$ y + 3x $y^{2}$ – $y^{3}$ + $y^{3}$ + 3.x $y^{2}$ + 3 $x^{2}$ .y + $x^{3}$ + $y^{3}$ – 3x. $y^{2}$ + 3 $x^{2}$ .y – $x^{3}$ – 3 $x^{2}$ y – 3x $y^{2}$

= ( $x^{3}$ + $x^{3}$ – $x^{3}$ )+ ( - 3 $x^{2}$ y + 3 $x^{2}$ y+ 3 $x^{2}$ y – 3 $x^{2}$ y)+ (3x $y^{2}$ + 3x $y^{2}$ - 3x $y^{2}$ - 3x $y^{2}$ ) + (- $y^{3}$ + $y^{3}$ + $y^{3}$ )

= $x^{3}$ + 0 $x^{2}$ y + 0.x $y^{2}$ + $y^{3}$

= $x^{3}$ + $y^{3}$

Câu 32:

Rút gọn biểu thức: P = 12.( $5^{2}$ + 1)( $5^{4}$ + 1)( $5^{8}$ + 1)( $5^{16}$ + 1)

Xem đáp án

Ta có:

( $5^{2}$ - 1).P = ( $5^{2}$ – 1).12.( $5^{2}$ + 1)( $5^{4}$ + 1)( $5^{8}$ + 1)( $5^{16}$ + 1)

= 12.( $5^{2}$ – 1).( $5^{2}$ + 1)( $5^{4}$ + 1)( $5^{8}$ + 1)( $5^{16}$ + 1)

= 12.( $5^{4}$ - 1)( $5^{4}$ + 1)( $5^{8}$ + 1)( $5^{16}$ + 1)

= 12.( $5^{8}$ - 1)( $5^{8}$ + 1)( $5^{16}$ + 1)

= 12.( $5^{16}$ - 1)( $5^{16}$ + 1)

= 12.( $5^{32}$ - 1)

Câu 33:

Chứng minh hằng đẳng thức: ${(a + b + c)}^{3}$ = $a^{3}$ + $b^{3}$ + $c^{3}$ + 3(a+b)(b+c)(c+a)

Xem đáp án

Biến đổi vế trái:

${(a + b + c)}^{3}$ = ${[(a +) + c]}^{3}$ = ${(a + b)}^{3}$ +3 ${(a + b)}^{2}$ c+3(a+b) $c^{2}$ + $c^{3}$

= $a^{3}$ + 3 $a^{2}$ b + 3a $b^{2}$ + $b^{3}$ + 3( $a^{2}$ + 2ab + $b^{2}$ )c + 3a $c^{2}$ + 3b $c^{2}$ + $c^{3}$

= $a^{3}$ + 3 $a^{2}$ b + 3a $b^{2}$ + $b^{3}$ + 3 $a^{2}$ c + 6abc + 3 $b^{2}$ c + 3a $c^{2}$ + 3b $c^{2}$ + c3

= $a^{3}$ + $b^{3}$ + $c^{3}$ + 3 $a^{2}$ b + 3a $b^{2}$ + 3 $a^{2}$ c + 6abc + 3 $b^{2}$ c + 3a $c^{2}$ + 3b $c^{2}$

= $a^{3}$ + $b^{3}$ + $c^{3}$ + (3 $a^{2}$ b + 3a $b^{2}$ ) +( 3 $a^{2}$ c + 3abc)+ (3abc + 3 $b^{2}$ c)+(3a $c^{2}$ + 3b $c^{2}$ )

= $a^{3}$ + $b^{3}$ + $c^{3}$ + 3ab(a + b) + 3ac(a + b) + 3bc(a + b) + 3 $c^{2}$ (a + b)

= $a^{3}$ + $b^{3}$ + $c^{3}$ + 3(a + b)(ab + ac + bc + $c^{2}$ )

= $a^{3}$ + $b^{3}$ + $c^{3}$ + 3(a + b)[a(b + c) + c(b + c)]

= $a^{3}$ + $b^{3}$ + $c^{3}$ + 3(a + b)(b + c)(a + c) (đpcm)

Bắt đầu thi ngay

CHỌN BỘ SÁCH BẠN MUỐN XEM

Giải Sách Bài Tập Toán 8 Tập 1

Bài 3, 4, 5: Những hằng đẳng thức đáng nhớ

Danh sách câu hỏi

Bài thi liên quan