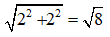- Đề số 1
- Đề số 2
- Đề số 3
- Đề số 4
- Đề số 5
- Đề số 6
- Đề số 7
- Đề số 8
- Đề số 9
- Đề số 10
- Đề số 11
- Đề số 12
- Đề số 13
- Đề số 14
- Đề số 15
- Đề số 16
- Đề số 17
- Đề số 18
- Đề số 19
- Đề số 20
- Đề số 21
- Đề số 22
- Đề số 23
- Đề số 24
- Đề số 25
- Đề số 26
- Đề số 27
- Đề số 28
- Đề số 29
- Đề số 30
- Đề số 31
- Đề số 32
- Đề số 33
- Đề số 34
- Đề số 35
- Đề số 36
- Đề số 37
- Đề số 38
- Đề số 39
- Đề số 40
- Đề số 41
Bài 12: Toán 8 Hình vuông
-
7205 lượt thi
-
21 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
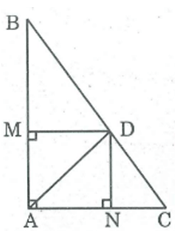
Cho tam giác ABC vuông tại A, đường phân giác AD. Gọi M, N là chân đường vuông góc kẻ từ D đến AB, AC. Chứng minh rằng tứ giác AMDN là hình vuông.
 Xem đáp án
Xem đáp án
Xét tứ giác AMDN, ta có: (MAN) = (gt)
DM ⊥ AB (gt)
⇒(AMD) =
DN ⊥ AC (gt) ⇒(AND) =
Suy ra tứ giác AMDN là hình chữ nhật
(vì có ba góc vuông), có đường chéo AD là đường phân giác của A
Vậy hình chữ nhật AMDN là hình vuông
Câu 2:
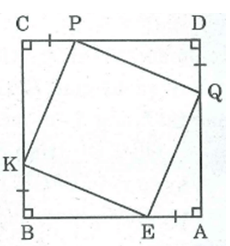
Cho hình vuông ABCD. Trên AB, BC, CD, DA lấy theo thứ tự các điểm E, K, P, Q sao cho AE = BK = CP = DQ. Tứ giác EKPQ là hình gì? Vì sao?
 Xem đáp án
Xem đáp án
Ta có: AB = BC = CD = DA (gt)
AE = BK = CP = DQ (gt)
Suy ra: EB = KC = PD = QA
* Xét ΔAEQ và ΔBKE,ta có:
AE = BK (gt)
(EAQ) = (KBE) =
QA = EB (chứng minh trên)
Suy ra: AEQ = BKE (c.g.c) ⇒ EQ = EK (1)
* Xét BKEvà CPK,ta có: BK = CP (gt)
(KBE) = (PCK) =
EB = KC ( chứng minh trên)
Suy ra: BKE = CPK (c.g.c) ⇒ EK = KP (2)
* Xét CPK và DQP,ta có: CP = DQ (gt)
C = D =
DP = CK ( chứng minh trên)
Suy ra: CPK = DQP (c.g.c) ⇒ KP = PQ (3)
Từ (1), (2) và (3) suy ra: EK = KP = PQ = EQ
Hay tứ giác EKPQ là hình thoi.
Mặt khác: AEQ = BKE
⇒ (AQE) = (BEK)
Mà (AQE) + (AEQ) =
⇒ (BEK) + (AEQ) =
Ta có: (BEK) + (QEK) + (AEQ ) =
Suy ra: (QEK ) = -( (BEK ) + (AEQ) )= - =
Vậy tứ giác EKPQ là hình vuông.
Câu 3:
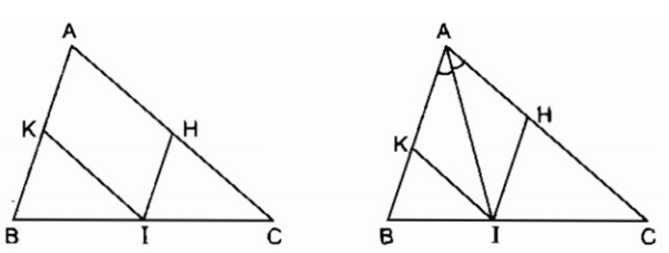
Cho tam giác ABC, điểm I nằm giữa B và C. Qua I vẽ đường thẳng song song với AB, cắt AC ở H. Qua I vẽ đường thẳng song song với AC, cắt AB ở K. Tứ giác AHIK là hình gì?
 Xem đáp án
Xem đáp án
Ta có: IK // AC (gt) hay IK // AH
Lại có: IH // AB (gt) hay IH // AK
Vậy tứ giác AHIK là hình bình hàn
Câu 4:
Cho tam giác ABC, điểm I nằm giữa B và C. Qua I vẽ đường thẳng song song với AB, cắt AC ở H. Qua I vẽ đường thẳng song song với AC, cắt AB ở K. Điểm I ở vị trí nào trên BC thì tứ giác AHIK là hình thoi
 Xem đáp án
Xem đáp án
Hình bình hành AHIK là hình thoi nên đường chéo AI là phân giác của (BAC)
Ngược lại nếu AI là phân giác của (BAC) thì hình bình hành AHIK có đường chéo AI là phân giác của một góc nên hình bình hành AHIK là hình thoi.
Vậy nếu I là giao điểm của đường phân giác của A với cạnh BC thì tứ giác AHIK là hình thoi.
Câu 5:
Cho tam giác ABC, điểm I nằm giữa B và C. Qua I vẽ đường thẳng song song với AB, cắt AC ở H. Qua I vẽ đường thẳng song song với AC, cắt AB ở K. Tam giác ABC có điều kiện gì thì tứ giác AHIK là hình chữ nhật.
 Xem đáp án
Xem đáp án
Hình bình hành AHIK là hình chữ nhật
⇒ A = suy ra ABC vuông tại A. Ngược lại ΔABC có A =
Suy ra hình bình hành AHIK là hình chữ nhật
Vậy nếu ABC vuông tại A thì tứ giác AHIK là hình chữ nhật.
Câu 6:
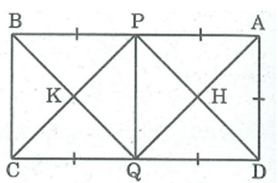
Hình chữ nhật ABCD có AB = 2AD. Gọi P, Q theo thứ tự là trung điểm của AB, CD. Gọi H là giao điểm của AQ và DP, gọi K là giao điểm của CP và BQ. Chứng minh rằng PHQK là hình vuông.
 Xem đáp án
Xem đáp án
* Xét tứ giác APQD, ta có: AB // CD (gt) hay AP // QD
AP = 1/2 .AB (gt)
QD = 1/2 CD (gt)
AB= CD (vì ABCD là hình chữ nhật)
Suy ra: AP = QD
Hay tứ giác APQD là hình bình hành.
Lại có: A = (vì tứ giác ABCD là hình chữ nhật)
Suy ra tứ giác APQD là hình chữ nhật.
Mà AD = AP = 1/2 AB
Vậy tứ giác APQD là hình vuông.
⇒ AQ ⊥ PD (t/chất hình vuông) ⇒ (PHQ) = (1)
HP = HQ (t/chất hình vuông)
* Xét tứ giác PBCQ, ta có: AB // CD hay BP //CQ
PB = 1/2 AB (gt)
CQ = 1/2 CD (gt)
AB = CD do ABCD là hình chữ nhật
Suy ra: PB = CQ nên tứ giác PBCQ là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau)
Lại có: B = (vì ABCD là hình chữ nhật) suy ra tứ giác PBCQ là hình chữ nhật
PB = BC ( vì cùng bằng AD = 1/2 AB)
Vậy tứ giác PBCQ là hình vuông
⇒ PC ⊥ BQ (t/chất hình vuông) ⇒ (PKQ) = (2)
PD là tia phân giác (APQ) ( t/chất hình vuông)
PC là tia phân giác (QPB) (t/chất hình vuông)
Suy ra: PD ⊥ PC (t/chất tia phân giác của hai góc kề bù) ⇒ (HPK) = (3)
Từ (1), (2) và (3) suy ra tứ giác PHQK là hình vuông.
Câu 7:
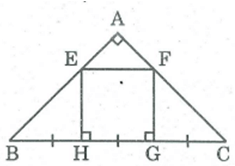
Cho tam giác ABC vuông cân tại A. Trên cạnh BC lấy các điểm H, G sao cho BH = HG = GC. Qua H và G kẻ các đường vuông góc với BC chúng cắt AB, AC theo thứ tự ở E và F. Tứ giác EFGH là hình gì? Vì sao?
 Xem đáp án
Xem đáp án
Vì ΔABC vuông cân tại A nên B = C =
Vì ΔBHE vuông tại H có B = nên ΔBHE vuông cân tại H.
Suy ra HB = HE
Vì ΔCGF vuông tại G, có C = nên ΔCGF vuông cân tại G
Suy ra GC = GF
Ta có: BH = HG = GC (gt)
Suy ra: HE = HG = GF
Vì EH // GF (hai đường thẳng cũng vuông góc với đường thắng thứ ba) nên tứ giác HEFG là hình bình hành (vì có một cặp cạnh đối song song bằng nhau);
Lại có (EHG) = nên HEFG là hình chữ nhật.
Mà EH = HG (chứng minh trên).
Vậy HEFG là hình vuông.
Câu 8:
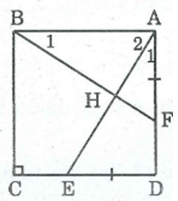
Cho hình vuông ABCD. Trên cạnh AD lấy điểm F, trên cạnh DC lấy điểm E sao cho AF = DE. Chứng minh rằng AE = BF và AE ⊥ BF.
 Xem đáp án
Xem đáp án
Xét ABF và DAE,ta có: AB = DA (gt)
(BAF) = (ADE) =
AF = DE (gt)
Suy ra: ΔABF = ΔDAE (c.g.c)
⇒ BF = AE và =
Gọi H là giao điểm của AE và BF.
Ta có: (BAF) = + =
Suy ra: + =
Trong ΔABH,ta có: (AHB) + + =
⇒ ((AHB) ) = – (+ ) = – =
Vậy AE ⊥ BF
Câu 9:
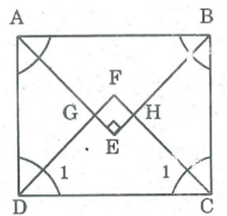
Cho hình chữ nhật có hai cạnh kề không bằng nhau. Chứng minh rằng các tia phân giác của các góc của hình chữ nhật đó cắt nhau tạo thành một hình vuông.
 Xem đáp án
Xem đáp án
Gọi giao điểm các đường phân giác của các góc: A, B, C, D theo thứ tự cắt nhau tại E, H, F, G.
* Trong ADG , ta có:
(GAD) = ; (GDA) = (gt)
Suy ra: (AGD) = - (GAD) - (GDA) =
⇒ GAD vuông cân tại G.
⇒ GD = GA
Trong BHC, ta có:
(HBC) = ; (HCB) = (gt)
Suy ra: (BHC) = - (HBC) - (HCB) =
⇒ HBC vuông cân tại H.
⇒ HB = HC
* Trong ΔFDC, ta có: = ; = (gt)
Suy ra: F = - D1 - C1 =
⇒ FDC vuông cân tại F ⇒ FD = FC
Nên tứ giác EFGH là hình chữ nhật (vì có 3 góc vuông).
Xét GAD và HBC,ta có: (GAD) = (HBC) =
AD = BC (tính chất hình chữ nhật)
(GDA) = (HCB) =
Suy ra: GAD = HBC ( g.c.g)
Do đó, GD = HC .
Lại có: FD = FC (chứng minh trên)
Suy ra: FG = FH
Vậy hình chữ nhật EFGH có hai cạnh kề bằng nhau nên nó là hình vuông.
Câu 10:
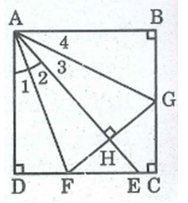
Cho hình vuông ABCD. Gọi E là một điểm nằm giữa C và D. Tia phân giác của góc DAE cắt CD ở F. Kẻ FH ⊥ AE (H ∈ AE) , FH cắt BC ở G. Tính số đo góc (FAG)
 Xem đáp án
Xem đáp án
* Xét hai tam giác vuông DAF và HAF, ta có:
(ADF) = (AHF) =
= (vì AF là tia phân giác của góc DAH)
AF cạnh huyền chung
Suy ra: DAF = HAF (cạnh huyền, góc nhọn)
⇒ DA = HA
Mà DA = AB (gt)
Suy ra: HA = AB
* Xét hai tam giác vuông HAG và, BAG, ta có:
(AHG) = (ABG) =
HA = AB (chứng minh trên)
AG cạnh huyền chung
Suy ra: HAG = BAG (cạnh huyền, cạnh góc vuông)
⇒ = hay AG là tia phân giác của (EAB)
Vậy (FAG) = + = 1/2 ((DAE) + (EAB) ) = 1/2 . =
Câu 11:
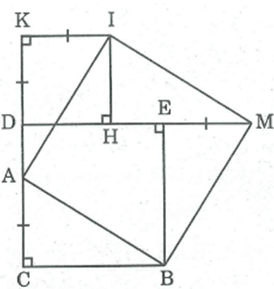
Cho hình vuông DEBC. Trên cạnh DC lấy điểm A, trên tia đối của tia DC lấy điểm K, trên tia đối của tia ED lấy điểm M sao cho CA = DK = EM . Vẽ hình vuông DKIH (H thuộc cạnh DE). Chứng minh rằng ABMI là hình vuông.
 Xem đáp án
Xem đáp án
* Xét CAB và EMB, ta có:
CA = EM (gt)
(ACB) = (MEB) =
CB = EB (tính chất hình vuông)
Suy ra: CAB = EMB (c.g.c)
⇒ AB = MB (1)
Ta có: AK = DK+ DA
CD = CA + AD
Mà CA = DK nên AK = CD
* Xét CAB và KIA, ta có:
CA = KI (vì cùng bằng DK)
C = K =
CB = AK (vì cùng bằng CD)
Suy ra: CAB = KIA (c.g.c)
⇒ AB = AI (2)
Ta có: DH = DK (vì KDHI là hình vuông)
Và EM = DK (gt)
Suy ra: DH = EM
⇒ DH + HE = HE + EM
Hay DE = HM
* Xét HIM và EMB, ta có: HI = EM (vì cũng bằng DK)
H = E =
HM = EB (vì cùng bằng DE)
Suy ra: HIM = EMB (c.g.c)
⇒ IM = MB (3)
Từ (1) , (2) và (3) suy ra: AB = BM = AI = IM
Tứ giác ABMI là hình thoi.
Mặt khác, ta có ACB = MEB (chứng minh trên)
⇒ (CBA) = (EBM)
Mà (CBA) + (ABE) = (CBE) =
Suy ra: (EBM) + (ABE) = hay (ABM) =
Vậy tứ giác ABMI là hình vuông.
Câu 12:
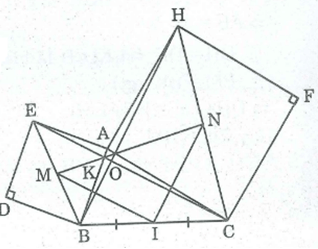
Cho tam giác ABC. Vẽ ở ngoài tam giác các hình vuông ABDE, ACFH. Chứng minh rằng EC = BH, EC ⊥ BH
 Xem đáp án
Xem đáp án
Ta có: (BAH) = (BAC) + (CAH) = (BAC) +
(EAC) = (BAC) + (BAE) = (BAC) +
Suy ra: (BAH) = (EAC)
* Xét BAH và EAC , ta có:
BA = EA (vì ABDE là hình vuông)
(BAH) = (EAC) (chứng minh trên)
AH = AC (vì ACFH là hình vuông)
Suy ra: BAH = EAC (c.g.c) ⇒ BH = EC
Gọi K và O lần lượt là giao điểm của EC với AB và BH.
Ta có: (AEC) = (ABH) (vì BAH = EAC) (1)
Hay (AEK) = (OBK)
* Trong AEK, ta có: (EAK) =
⇒ (AEK) + (AKE) = (2)
Mà (AKE) = (OKB) (đối đỉnh) (3)
Từ (1), (2) và (3) suy ra:
(OKB) + (OBK) =
* Trong Δ BOK ta có:
(BOK) + (OKB) + (OBK) =
⇒ (BOK) = – ((OKB) + (OBK) ) = – =
Suy ra: EC ⊥ BH
Câu 13:
Cho tam giác ABC. Vẽ ở ngoài tam giác các hình vuông ABDE, ACFH. Gọi M, N theo thứ tự là tâm của các hình vuông ABDE, ACFH. Gọi I là trung điểm của BC. Tam giác MIN là tam giác gì? Vì sao?
 Xem đáp án
Xem đáp án
* Trong EBC , ta có: M là trung điểm EB (tính chất hình vuông)
I trung điểm BC (gt)
Nên MI là đường trung bình của ΔEBC
⇒ MI = 1/2 EC và MI // EC (tính chất đường trung bình của tam giác).
Trong BCH, ta có: I trung điểm BC (gt)
N trung điểm của CH (tính chất hình vuông)
Nên NI là đường trung bình của BCH
⇒ NI = 1/2 BH và NI // BH (tính chất đường trung bình của tam giác)
Mà BH = CE (chứng minh trên)
Suy ra: MI = NI nên INM cân tại I
MI // EC (chứng minh trên)
EC ⊥ BH (chứng minh trên)
Suy ra: MI ⊥ BH. Mà NI // BH (chứng minh trên)
Suy ra: MI ⊥ NI hay (MIN) =
Vậy MIN vuông cân tại I.
Câu 14:
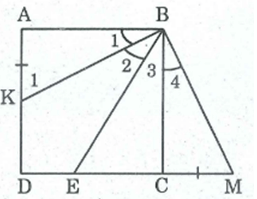
Cho hình vuông ABCD, điểm E thuộc cạnh CD. Tia phân giác của góc ABE cắt AD ở K. Chứng minh rằng AK+CE = BE.
 Xem đáp án
Xem đáp án
Trên tia đối của tia CD lấy điểm M sao cho CM = AK
Ta có: AK + CE = CM + CE = EM (1)
Xét ABK và CBM, ta có:
AB = CB (gt)
A = C =
AK = CM (theo cách vẽ)
Suy ra: ABK = CBM (c.g.c)
⇒ = (2)
Lại có: = ( do BK là tia phân giác của ABE)
Suy ra: = =
Mà (KBC) = - (3)
Tam giác CBM vuông tại C nên: M = - (4)
Từ (2), (3) và (4) suy ra: (KBC) = M (5)
Hay + = M
⇒ + = M( vì = )
Hay: (EBM) = M
⇒ EBM cân tại E ⇒ EM = BE. (6)
Từ (1) và (6) suy ra: AK + CE = BE.
Câu 15:
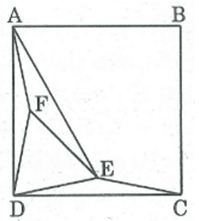
Cho hình vuông ABCD. Gọi E, F theo thứ tự là trung điểm của AB, BC. Chứng minh rằng CE vuông góc với DF.
 Xem đáp án
Xem đáp án
Xét BEC và CFD , ta có: BE = CF (gt)
B = C =
BC = CD (gt)
Suy ra: BEC = CFD (c.g.c) ⇒ ∠C1 = ∠D1
Lại có: + =
Suy ra: + =
Trong ΔDCM có + =
Suy ra: (DMC) =
Vậy CE ⊥ DF
Câu 16:
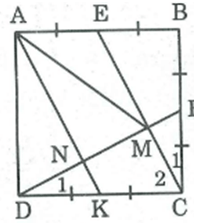
Cho hình vuông ABCD. Gọi E, F theo thứ tự là trung điểm của AB, BC. Gọi M là giao điểm của CE và DF. Chứng minh rằng AM = AD.
 Xem đáp án
Xem đáp án
Gọi K là trung điểm của DC, AK cắt DF tại N.
* Xét tứ giác AKCE, ta có: AB // CD hay AE // CK
AE = 1/2 AB (gt)
CK = 1/2 CD (theo cách vẽ)
AB = CD ( Vì ABCD là hình vuông)
Suy ra: AE = CK nên tứ giác AKCE là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau) ⇒ AK// CE
DF ⊥ CE (chứng minh trên) ⇒ AK ⊥ DF hay AN ⊥ DM
* Trong DMC, ta có: DK = KC và KN // CM
Nên DN = MN (tính chất đường trung bình của tam giác)
Tam giác ADM có AN là đường cao đồng thời là đường trung tuyến
Suy ra: ADM cân tại A
Vậy AD = AM.
Câu 17:
Cho hình vuông ABCD. Vẽ điểm E trong hình vuông sao cho (EDC) = (ECD) =
Vẽ điểm F trong hình vuông sao cho (FAD) = (FDA) = . Chứng minh rằng tam giác DEF là tam giác đều.
 Xem đáp án
Xem đáp án
Xét EDC và FDA, tacó: (EDC) = (FDA) =
DC = AD (gt)
(ECD) = (FAD) =
Suy ra: EDC = FDA (g.c.g)
⇒ DE = DF
⇒ DEF cân tại D
Lại có: (ADC) = (FDA) + (FDE) + (EDC)
⇒ (FDE) = (ADC) -((FDA) + (EDC) )= - ( + ) =
Vậy DEF đều.
Câu 18:
Cho hình vuông ABCD. Vẽ điểm E trong hình vuông sao cho (EDC) = (ECD) =
Chứng minh rằng tam giác ABE là tam giác đều.
 Xem đáp án
Xem đáp án
Xét ADE và BCE , ta có:
ED = EC (vì AEDC cân tại E)
(ADE) = (BCE) =
AD = BC (gt)
Suy ra: ADE = BCE (c.g.c)
⇒ AE = BE (1)
* Trong ADE, ta có:
(AFD) = – ((FAD) + (FDA) ) = – ( + ) =
(AFD) + (DFE) + (AFE) =
⇒ (AFE) = - ((AFD) + (DFE) ) = – ( + ) =
* Xét AFD và AFE, ta có: AF cạnh chung
(AFD) = (AFE) =
DE = EF (vì DFE đều)
Suy ra: AFD = AFE (c.g.c) ⇒ AE = AD
Mà AD = AB (gt)
Suy ra: AE = AB (2)
Từ (1) và (2) suy ra: AE = AB = BE
Vậy AEB đều.
Câu 19:
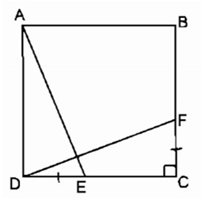
Hình vuông có chu vi bằng 8 thì đường chéo bằng :
A. 2
B.
C.
D.
Hãy chọn phương án đúng.
 Xem đáp án
Xem đáp án
Chọn C. Đúng
Cạnh hình vuông = 8:4=2
Đường chéo =
Câu 20:
Cho hình thoi ABCD, O là giao điểm của hai đường chéo. Các tia phân giác của bốn góc vuông có đỉnh O cắt các cạnh AB, BC, CD, DA theo thứ tự ở E, F, G, H. Tứ giác EFGH là hình gì ?
 Xem đáp án
Xem đáp án
Ta có: (AOB) và (COD) đối đỉnh nên E, O, G thẳng hàng
(BOC) và (AOD) đối đỉnh nên F, O, H thẳng hàng
Xét BEO và BFO:
(EBO) = (FBO) (tính chất hình thoi)
OB cạnh chung
(EOB) = (FOB) = (gt)
Do đó: BEO = BFO (g.c.g)
⇒ OE = OF (1)
Xét BEO và DGO:
(EBO) = (GDO) (so le trong)
OB = OD(tính chất hình thoi)
(EOB) = (GOD) (đối đỉnh)
Do đó: BEO = DGO (g.c.g)
⇒ OE = OG (2)
Xét AEO và AHO:
(EAO) = (HAO) (tính chất hình thoi)
OA cạnh chung
(EOA) = (HOA) = (gt)
Do đó: AEO = AHO (g.c.g)
⇒ OE = OH (3)
Từ (1), (2) và (3) suy ra: OE = OF = OG = OH hay EG = FH
nên tứ giác EFGH là hình chữ nhật (vì có hai đường chéo cắt nhau tại trung điểm mỗi đường và bằng nhau)
OE ⊥ OF (tính chất tia phân giác của hai góc kề bù)
hay EG ⊥ FH
Vậy hình chữ nhật EFGH là hình vuông.
Câu 21:
Cho hình vuông ABCD. Trên cạnh DC lấy điểm E, trên cạnh BC lấy điểm F sao cho DE = CF. Chứng minh rằng AE = DF và AE ⊥ DF.
 Xem đáp án
Xem đáp án
Xét ADE và DCF:
AD = DC (gt)
A = D =
DE = CF (gt)
Do đó: ADE = DCF (c.g.c)
⇒ AE = DF
(EAD) = (FDC)
(EAD) + (DEA) = (vì ΔADE vuông tại A)
⇒(FDC) + (DEA) =
Gọi I là giao điểm của AE và DF.
Suy ra: (IDE) + (DEI) =
Trong DEI ta có: (DIE) = – ((IDE) + (DEI) ) = – =
Suy ra: AE ⊥ DF