8 câu hỏi trắc nghiệm thuộc Bài 6: Toán 8 Diện tích đa giác (tập 1)

Giải Sách Bài Tập Toán 8 Tập 1

Đề số 1
Đề số 2
Đề số 3
Đề số 4
Đề số 5
Đề số 6
Đề số 7
Đề số 8
Đề số 9
Đề số 10
Đề số 11
Đề số 12
Đề số 13
Đề số 14
Đề số 15
Đề số 16
Đề số 17
Đề số 18
Đề số 19
Đề số 20
Đề số 21
Đề số 22
Đề số 23
Đề số 24
Đề số 25
Đề số 26
Đề số 27
Đề số 28
Đề số 29
Đề số 30
Đề số 31
Đề số 32
Đề số 33
Đề số 34
Đề số 35
Đề số 36
Đề số 37
Đề số 38
Đề số 39
Đề số 40
Đề số 41

Bài 6: Toán 8 Diện tích đa giác (tập 1)

7183 lượt thi
8 câu hỏi
30 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

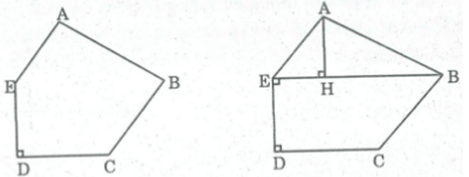
Thực hiện phép vẽ và đo cần thiết để tính diện tích đa giác ABCDE có AE // BC (như hình vẽ).

Xem đáp án

Chia đa giác ABCDE thành $∆$ ABE và hình thang vuông BEDC.

Kẻ AH ⊥ BE .

Dùng thước chia khoảng đo độ dài: BE, DE, CD, AH.

Ta có: $S_{A B C D E} = S_{A B E} + S_{B E D C}$

Câu 2:

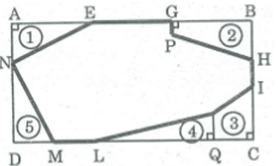
Theo bản đồ ghi hình bên tỉ lệ 1:100 , hãy tính điện tích hồ nước phần gạch đậm.

Xem đáp án

Giả sử hình chữ nhật là ABCD.

Trên AB, 2 giao điểm là E và G.

Trên BC hai giao điểm là I và H.

Trên CD hai giao điểm là L và M. Giao điểm trên AD là N. Hình thang tại đỉnh B có giao điểm là P, điểm trên đường gấp khúc IL là K.

Kẻ KQ ⊥ CD, gọi điện tích phẩn gạch đậm là S.

Ta có: S = $S_{A B C} - S_{A N E} - S_{B H P G} - S_{I C Q K} - S_{D M N}$

Dùng thước chia khoảng đo các đoạn (mm):

AB, AD, AE, AN, PG, GB, BH, IC, CQ, QK, LQ, DM

Câu 3:

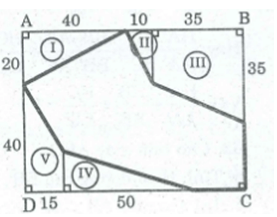
Theo kích thước đã cho trên hình. Tính diện tích phân gạch đậm (đơn vị là $m^{2}$ )

Xem đáp án

SABCD = AD.AB = (20 + 40).(40 + 10 + 35) = 5100 ( $m^{2}$ )

$S_{I}$ = 1/2 .40.20 = 400 ( $m^{2}$ )

$S_{I I}$ = 1/2 .10.20 = 100 ( $m^{2}$ )

$S_{I I I}$ = 1/2 (20 + 35).35 = 962,5 ( $m^{2}$ )

$S_{I V}$ = 1/2 .15.50 = 375 (m2)

$S_{V}$ = 1/2 (15 + 40).15 = 412,5 ( $m^{2}$ )

Diện tích phần gạch đậm:

S = 5100 - (400 + 100 + 962,5 + 375 + 412,5) = 2850 ( $m^{2}$ )

Câu 4:

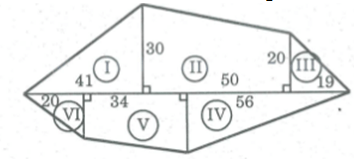
Tính diện tích mảnh đất theo kích thước trong hình (đơn vị $m^{2}$ )

Xem đáp án

$S_{I}$ = 1/2 .41.30 = 615 ( $m^{2}$ )

$S_{I I}$ = 1/2 (30 + 20).50 = 1250 ( $m^{2}$ )

$S_{I I I}$ = 1/2 .20.19 = 190 ( $m^{2}$ )

$S_{I V}$ = 1/2 .19.56 = 532 ( $m^{2}$ )

$S_{V}$ = 1/2 (19+16).34 = 595 ( $m^{2}$ )

$S_{V I}$ = 1/2 .16.20 = 160 ( $m^{2}$ )

S = $S_{I}$ + $S_{I I}$ + $S_{I I I}$ + $S_{I V}$ + $S_{V}$ + $S_{V I}$ ( $m^{2}$ )

= (615 + 1250 + 190 + 532 + 595 + 160) = 3342 ( $m^{2}$ ).

Câu 5:

Tính diện tích của hình được cho trong mỗi trường hợp sau đây: Đa giác ABCDEF, biết AD = 4cm, BC = 1cm, FE = 2cm, FB = 3cm, FB vuông góc với AD như hình bs. 24

Xem đáp án

Ta chia đa giác ABCDEF thành hai hình thang ABCD và ADEF.

Hình thang ABCD có cạnh đáy BC = 1 (cm)

Đáy AD = AG + GD = 1 + 3 = 4 (cm)

Đường cao BG = 1 (cm)

$S_{A B C D}$ = (AD + BC) / 2.FG = (4 + 1) / 2 = 5/2 ( $c m^{2}$ )

Hình thang ADEF có đáy AD = 4 (cm)

$S_{A D E F}$ = (AD + EF) / 2.FG = (4 + 2) / 2. 2 = 6 ( $c m^{2}$ )

$S_{A B C D E F}$ = $S_{A B C D}$ + $S_{A D E F}$ = 5/2 + 6 = 17/2 ( $c m^{2}$ )

Đáy EF = 2cm, đường cao FG = 2cm

Câu 6:

Tính diện tích của hình được cho trong mỗi trường hợp sau đây: Cho đa giác ABCD, CF và DE đều vuông góc với AB (như hình bs. 25)

Biết AB = 13cm, CF = 8cm, DE = 4cm, FB = 6cm và AE = 3cm. Tính diện tích đa giác ABCD

Xem đáp án

Chia đa giác ABCD thành tam giác vuông AED, hình thang vuông EDCF và tam giác vuông FCB.

$S_{A E D}$ = 1/2 AE.DE = 1/2. 3. 4 = 6( $c m^{2}$ )

$S_{E D C F}$ = (ED + FC)/2. EF = (4 + 8)/2. 4 = 24 ( $c m^{2}$ )

$S_{C F B}$ = 1/2 CF. FB = 1/2 .8 .6 = 24 ( $c m^{2}$ )

$S_{A B C D}$ = $S_{A E D}$ + $S_{E D C F}$ + $S_{C F B}$ = 6 + 24 + 24 = 54 ( $c m^{2}$ )

Câu 7:

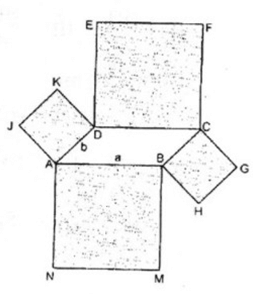
Cho hình bình hành ABCD, với diện tích S và AB = a, AD = b. Lấy mỗi cạnh của hình bình hành đó làm cạnh dựng một hình vuông ra phía ngoài hình bình hành. Tính theo a, b và S diện tích của đa giác giới hạn bởi các cạnh của hình vuông mà không là cạnh của hình bình hành đã cho.

Xem đáp án

Hình đa giác đó gồm hình bình hành ABCD, hình vuông ABMN, BHGC, CFED, DKJA.

$S_{A B M N} = S_{C D E F} = a^{2}$

$S_{B H G C} = S_{D K J A} = b^{2}$

Diện tích đa giác bằng :

$S_{A B M N} = S_{C D E F} = a^{2}$

$S_{B H G C} = S_{D K J A} = b^{2}$

Câu 8:

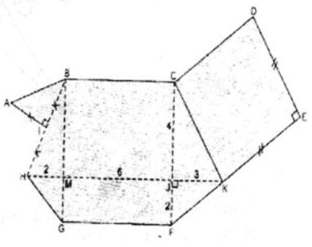
Bạn Giang đã vẽ một đa giác ABCDEFGHI như ở hình bs. 26.

Tính diện tích của đa giác đó, biết rằng : KH song song với BC (K thuộc EF); BC song song với GF; CF song song với BG; BG vuông góc với GF; CK song song với DE; CD song song với FE; KE = DE và KE vuông góc với DE; I là trung điểm của BH, AI = IH và AI vuông góc với IH; HK = 11cm, CF = 6cm. HK cắt CF tại J và JK = 3 (cm), JF = 2cm. BG cắt HK tại M và HM = 2cm.

Xem đáp án

Chia đa giác đó thành hình vuông CDEK, hình thang KFGH, hình thang BCKH và tam giác vuông AIB

Ta có: MJ = KH – KJ – MH = 11 – 2 – 3 = 6(cm)

⇒ BC = GF = MJ = 6 (cm)

CJ = CF – FG = 6 – 2 = 4 (cm)

$S_{K F G H}$ = (HK + GF)/2. FJ = (11 + 6)/2.2 = 17 ( $c m^{2}$ )

$S_{B C K H}$ = (BC + KH)/2. FJ = (11 + 6)/2.4 = 34 ( $c m^{2}$ )

Trong tam giác vuông BMH có $∠$ J = $90^{0}$ .Theo định lý Pi-ta-go ta có:

$C K^{2} = C J^{2} + J K^{2}$ = 16 + 9 = 25 ⇒ CK = 5 (cm)

$S_{C D E K} = C K^{2} = 5^{2}$ = 25 ( $c m^{2}$ )

Trong tam giác vuông BMH có $∠$ M = $90^{0}$ .Theo định lý Pi-ta-go ta có:

$B H^{2} = B M^{2} + H M^{2}$

mà BM = CJ = 4(cm) (đường cao hình thang BCKH)

⇒ $B H^{2} = 4^{2} + 2^{2}$ = 20

IB = BH/2 ⇒ $I B^{2} = B H^{2} / 2$ = 20/4 = 5

IB = $\sqrt{5}$ (cm)

$∆$ AIB vuông cân tại I (vì AI = IH = IB)

$S_{A I B}$ = 1/2 AI. IB = 1/2 $I B^{2}$ = 5/2 ( $c m^{2}$ )

S = $S_{C D E K} + S_{K F G H} + S_{B C K H} + S_{A I B}$ = 25 + 17 + 34 + 5/2 = 157/2 ( $c m^{2}$ )

Bắt đầu thi ngay

CHỌN BỘ SÁCH BẠN MUỐN XEM

Giải Sách Bài Tập Toán 8 Tập 1

Bài 6: Toán 8 Diện tích đa giác (tập 1)

Danh sách câu hỏi

Bài thi liên quan