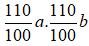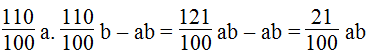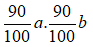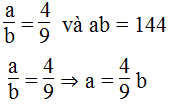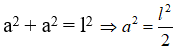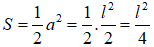30 câu hỏi trắc nghiệm thuộc Bài 2: Toán 8 Diện tích hình chữ nhật (tập 1) - hamchoi.vn

Giải Sách Bài Tập Toán 8 Tập 1

Bài 2: Toán 8 Diện tích hình chữ nhật (tập 1)

7167 lượt thi
30 câu hỏi
30 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

Diện tích hình chữ nhật thay đổi như thế nào: Chiều dài tăng 3 lần, chiều rộng không thay đổi?

Theo công thức tính diện tích hình chữ nhật S = ab thì diện tích của hình chữ nhật tỉ lệ thuận với chiếu dài và chiều rộng của hình chữ nhật đó. Gọi chiều dài-hình chữ nhật là a, chiều rộng là b, diện tích là S, chiếu dài mới a', chiều rộng b', diện tích S'.

Nếu a' = 3a, b' = b ⇒ S' = a'.b' = 3ab = 3S. Diện tích hình mới bằng 3 lần diện tích hình đã cho.

Câu 2:

Diện tích hình chữ nhật thay đổi như thế nào: Chiều rộng giảm 2 lần, chiều dài không thay đổi?

Theo công thức tính diện tích hình chữ nhật S = ab thì diện tích của hình chữ nhật tỉ lệ thuận với chiếu dài và chiều rộng của hình chữ nhật đó. Gọi chiều dài-hình chữ nhật là a, chiều rộng là b, diện tích là S, chiếu dài mới a', chiều rộng b', diện tích S'.

Nếu b' = 1/2 b, a' = a ⇒ S' =a'.b' = a. 1/2 b = 1/2 ab = 1/2 S

Diện tích hình mới bằng một nửa diện tích hình đã cho.

Câu 3:

Diện tích hình chữ nhật thay đổi như thế nào: Chiều dài và chiếu rộng đều tăng 4 lần?

Theo công thức tính diện tích hình chữ nhật S = ab thì diện tích của hình chữ nhật tỉ lệ thuận với chiếu dài và chiều rộng của hình chữ nhật đó. Gọi chiều dài-hình chữ nhật là a, chiều rộng là b, diện tích là S, chiếu dài mới a', chiều rộng b', diện tích S'.

Nếu a' = 4a, b' = 4b ⇒ S' = a'.b' = 4a.4b = 16ab = 16S.

Diện tích hình mới bằng 16 lần diện tích hình đã cho.

Câu 4:

Diện tích hình chữ nhật thay đổi như thế nào: Chiều dài tăng 4 lần, chiều rộng giảm 3 lần?

Theo công thức tính diện tích hình chữ nhật S = ab thì diện tích của hình chữ nhật tỉ lệ thuận với chiếu dài và chiều rộng của hình chữ nhật đó. Gọi chiều dài-hình chữ nhật là a, chiều rộng là b, diện tích là S, chiếu dài mới a', chiều rộng b', diện tích S'.

Nếu a' = 4a, b' = 1/3 b ⇒ S' = a'.b' = 4a.1/3 b = 4/3 ab = 4/3 S.

Diện tích hình mới bằng 4/3 diện tích hình đã cho.

Câu 5:

Cho hình chữ nhật có diện tích 20 (đơn vị diện tích) và hai kích thước x và y (đơn vị dài). Hãy điền vào ô trống trong bảng sau.

Câu 6:

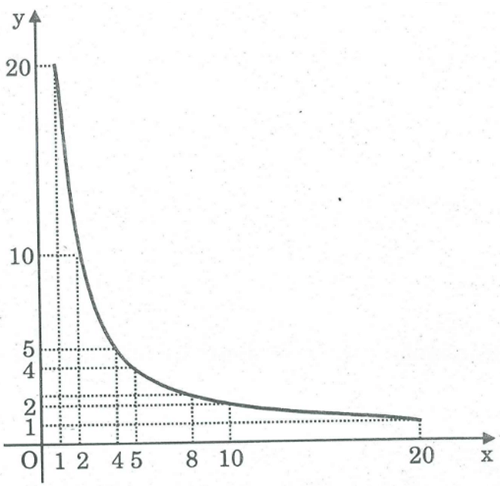
Cho hình chữ nhật có diện tích 20 (đơn vị diện tích) và hai kích thước x và y (đơn vị dài). Theo bảng vừa thành lập, hãy biểu diễn bảy điểm của đồ thị hàm số y = 20/x trên mặt phẳng tọa độ xOy

Vẽ hình

Câu 7:

Diện tích hình chữ nhật tăng bao nhiêu phần trăm nếu mỗi cạnh tăng 10%

Gọi chiều dài,chiều rộng của hình chữ nhật là a và b ( a> b >0).

Nếu mỗi cạnh tăng 10% thì độ dài mỗi cạnh sau khi tăng là:

Diện tích hình chữ nhật mới là:

Phần diện tích tăng thêm là:

Vậy diện tích tăng thêm 21% so với diện tích ban đầu.

Câu 8:

Diện tích hình chữ nhật giảm bạo nhiêu phần trăm nếu mỗi cạnh giảm 10%.

Nếu mỗi cạnh giảm đi 10% thì độ dài mỗi cạnh Sau khi giảm

Diện tích hình chữ nhật mới là:

Phần diện tích bị giảm đi là:

Vậy diện tích của hình giảm đi 19% so với diện tích hình ban đầu

Câu 9:

Diện tích của một hình chữ nhật bằng 48 $c m^{2}$ , một cạnh của nó có độ dài 8cm. Đường thẳng song song với một trong các cạnh của hình chữ nhật chia hình chữ nhật đó thành hai hình chữ nhật bằng nhau. Tính chu vi của mỗi hình chữ nhật được tạo thành.

Diện tích hình chữ nhật 48 $c m^{2}$ , một cạnh có độ dài bằng 8 cm, độ dài cạnh kia: 48 : 8 = 6 (cm)

a. Chia hình chữ nhật bởi trung điểm của chiều dài thì ta có hai hình chữ nhật bằng nhau có kích thước là 4 cm và 6cm.

Chu vi mỗi hình là: (4 + 6).2 = 20 (cm)

b. Chia hình chữ nhật bởi trung điểm của chiều rộng thì ta có hai hình chữ nhật bằng nhau có kích thước là 8 cm và 3 cm.

Chu vi mỗi hình là: (8 + 3).2 = 22 (cm)

Câu 10:

Tính các cạnh của một hình chữ nhật, biết bình phương của độ dài một cạnh bằng 16 và diện tích của hình chữ nhật bằng 28 $c m^{2}$

Gọi độ dài hai cạnh của hình chữ nhật là a và b (a > 0, b > 0)

Theo bài ra, giả sử ta có: $a^{2}$ = 16 và ab = 28

$a^{2}$ = 16 ⇒ a = 4 (cm) (vì a > 0) ⇒ b = 28 : a = 28 : 4 = 7 (cm)

Vậy hai kích thước là 4cm và 7cm.

Câu 11:

Tính các cạnh của một hình chữ nhật, biết tỉ số các cạnh là 4/9 và diện tích của nó là 144 $c m^{2}$

Gọi độ dài hai cạnh hình chữ nhật là a và b (0 < a < b)

Theo bài ta, ta có:

Suy ra: 4/9 b.b = 144 ⇒ $b^{2}$ = 144 : 4/9 = 144.9/4 = 324 = $18^{2}$

⇒ b = 18 (cm) ⇒ a = 4/9 . 18 = 8 (cm)

Câu 12:

Cho tam giác vuông cân, biết độ dài cạnh huyền là l. Tính diện tích tam giác đó.

Gọi độ dài cạnh góc vuông của tam giác vuông cân là a (0 < a < l)

Áp dụng định lí Pi-ta-go vào tam giác vuông ta có:

Diện tích tam giác vuông đó là:

Câu 13:

Tính diện tích các hình trong hình vẽ sau (mỗi ô vuông là một đơn vị diện tích). Hãy giải thích vì sao tính được như vậy.

Hình A cắt rời thành hai tam giác ghép lại được một hình chữ nhật có một cạnh 3 ô vuông và một cạnh 2 ô vuông nên có diện tích là 6 ô vuông (6 đơn vị diện tích)

Câu 14:

Tính diện tích các hình trong hình vẽ sau (mỗi ô vuông là một đơn vị diện tích). Hãy giải thích vì sao tính được như vậy.

Hình B là một hình thang cân, cắt theo đường cao kẻ từ một đỉnh của đáy nhỏ ghép lại tạ được một hình chữ nhật có một cạnh 3 ô vuông và một cạnh 2 ô vuông nên diện tích bằng 6 ô vuông (6 đơn vị diện tích).

Câu 15:

Tính diện tích các hình trong hình vẽ sau (mỗi ô vuông là một đơn vị diện tích). Hãy giải thích vì sao tính được như vậy.

Hình C là hình thang vuông, cắt phần nhọn ghép lên phẩn trên, ta được một hình chữ nhật có một cạnh là 3 ô vuông và một cạnh 2 ô vuông nên diện tích bằng 6 ô vuông (6 đơn vị diện tích).

Câu 16:

Tính diện tích các hình trong hình vẽ sau (mỗi ô vuông là một đơn vị diện tích). Hãy giải thích vì sao tính được như vậy.

Hình D ta lấy diện tích hình vuông có cạnh 5 ô vuông trừ đi phần khuyết của 4 góc mỗi góc là một nửa ô vuông ta có diện tích là 5 x 5 – 4. 1/2 = 25 – 2 = 23 ô vuông (23 đơn vị diện tích).

Câu 17:

Trên giấy ô vuông hãy vẽ: Hai hình chữ nhật có cùng chu vi khác diện tích.

Chu vi mỗi hình là 10 (đơn vị)

Diện tích hai hình lần lượt là: 3.2 = 6 và 4.1 = 4 ( đơn vị diện tích).

Câu 18:

Trên giấy ô vuông hãy vẽ: Hai hình chữ nhật có kích thước khác nhau nhưng có diện tích bằng nhau

Chu vi mỗi hình lần lượt là: ( 6+1).2 = 14 và ( 3+ 2).2 = 10 ( đơn vị).

Diện tích hai hình bằng nhau và bằng: 6.1 = 3.2= 6 ( đơn vị diện tích) .

Câu 19:

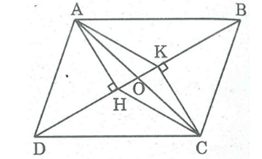
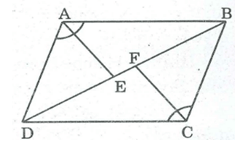
Cho hình bình hành ABCD (như hình vẽ). Từ A và C kẻ AH và CK vuông góc với đường chéo BD. Chứng minh.rằng hai đa giác ABCH và ADCK có cùng diện tích.

Ta có:

$△$ ABC = $△$ ADC (c.c.c) ⇒ $S_{A B C} = S_{A D C}$ (1)

$△$ AHC = $△$ AKC (c.c.c) ⇒ $S_{A H C} = S_{A K C}$ (2)

Từ (l) và (2) ⇒ $S_{A B C} + S_{A H C}$ = $S_{A D C} + S_{A K C}$

Hay $S_{A B C H} = S_{A D C K}$

Câu 20:

Cho hình bình hành ABCD. Đường phân giác của các góc A và C cắt đường chéo BD tại E, F. Chứng minh hai hình ABCFE và ADCFE có cùng diện tích.

Ta có:

$△$ ABE = $△$ CDF (g.c.g) ⇒ $S_{A B E} = S_{C D F}$ (l)

$△$ AED = $△$ CFB (g.c.g) ⇒ $S_{A E D} = S_{C F B}$ (2)

Từ (1) và (2) ⇒ $S_{A B E} + S_{C F B}$ = $S_{C D F} + S_{A E D}$

Hay $S_{A B C F E} = S_{A D C F E}$

Câu 21:

Cho hình bình hành ABCD. Đường phân giác của các góc A và C cắt đường chéo BD tại E, F. Các hình đó có phải là đa giác lồi không? Vì sao?

Hình ABCFE không phải là đa giác lồi vì nó nằm trên hai nửa mặt phẳng có bờ là đường thẳng chứa cạnh EF.

Hình ADCFE không phải là đa giác lồi vì nó nằm trên hai nửa mặt phẳng có bờ là đường thẳng chứa cạnh EF.

Câu 22:

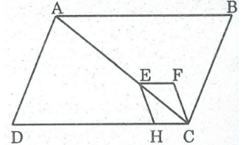
Trên hình vẽ bên dưới, các tứ giác ABCD, EFCH đều là hình bình hành. Điểm E nằm trên đường chéo AC. Chứng minh rằng đa giác AEHD và hình ABCFE có diện tích bằng nhau

Ta có:

$△$ ABC = $△$ CDA (c.c.c) ⇒ $S_{A B C} = S_{C D A}$ (1)

$△$ EFC = $△$ CHE (c.c.c) ⇒ $S_{E F C} = S_{C H E}$ (2)

Từ (1) và (2) ⇒ $S_{A B C} - S_{E F C}$ = $S_{C D A} - S_{C H E}$

Hay $S_{A B C F E} = S_{A E H D}$

Câu 23:

Trên hình vẽ bên dưới, các tứ giác ABCD, EFCH đều là hình bình hành. Điểm E nằm trên đường chéo AC. ABCFE có phải là đa giác lồi không? Vì sao?

Hình ABCFE không phải là tứ giác lồi vì nó nằm trên hai nửa mặt phẳng có bờ là đường thẳng chứa cạnh CF.

Câu 24:

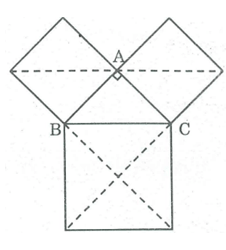
Cho một tam giác vuông cân. Chứng minh rằng tổng diện tích của hai hình vuông dựng trên hai cạnh góc vuông bằng diện tích hình vuông dựng trên cạnh huyền.

Gọi S là diện tích của tam giác ABC.

Hình vuông có cạnh AB được chia thành hai tam giác vuông cân bằng $△$ ABC nên diện tích hình vuông cạnh AB bằng 2S.

Hình vuông có cạnh AC được chia thành hai tam giác vuông cân bằng $△$ ABC nên diện tích hình vuông cạnh AC bằng 2S.

Hình vuông cạnh BC được chia thành bốn hình tam giác vuông cân bằng $△$ ABC nên có diện tích bằng 4S.

Vì 4S = 2S + 2S nên diện tích hình vuông dựng trên cạnh huyền bằng tổng diện tích hai hình vuông dựng trên hai cạnh góc vuông.

Câu 25:

Nền của một phòng học có dạng hình chữ nhật, với chiều rộng đo được là 4m và chiều dài là 6m. Để có thể lát kín nền đó cần bao nhiêu viên gạch có hình vuông, với cạnh là 33,33cm ?

Diện tích nền phòng học : 4.6 = 24 ( $m^{2}$ )

Số viên gạch cần dùng : 24: ${(0, 3333)}^{2}$ ≈ 216 (viên)

Câu 26:

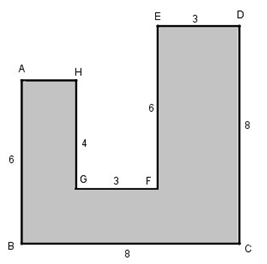
Cần bao nhiêu viên gạch có hình vuông, với cạnh là 25cm để có thể lát kín một mảnh sân có dạng như hình bs. 23 (biết AB = 6cm, BC = 8m, CD = 8m, DE = 3m, EF = 6m, FG = 3m, GH = 4m và góc tại các đỉnh A, B, C, D, E, F, G, H đều là góc vuông) ?

Diện tích của mảnh sân đó là: 12 + 6 + 24 = 42 ( $m^{2}$ ).

Viên gạch hình vuông có độ dài cạnh là: 25 cm = 0,15m

Diện tích 1 viên gạch là: $0, 25^{2}$

Do đó, để lát hết mảnh sân đó cần dùng số viên gạch là: 42: $0, 25^{2}$ = 672 viên gạch

Câu 27:

Dùng diện tích để chứng tỏ : ${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$

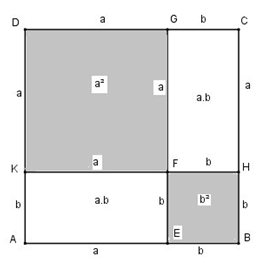
Dựng hình vuông ABCD có cạnh bằng (a + b )

Trên cạnh AB dựng điểm E sao cho AE = a, EB = b, trên cạnh BC dựng điểm H sao cho BH = b, HC = a, trên cạnh CD dựng điểm G sao cho CG = b, GD = a, trên cạnh DA dựng điểm K sao cho DK = a, KA = b, GE cắt KH tại F.

Ta có : diện tích hình vuông ABCD bằng ${(a + b)}^{2}$

Diện tích hình vuông DKFG bằng $a^{2}$

Diện tích hình chữ nhật AKFE bằng a.b

Diện tích hình vuông EBHF bằng $b^{2}$

Diện tích hình chữ nhật HCGF bằng a.b

$S_{A B C D} = S_{D K F G} + S_{A K E F} + S_{E B H F} + S_{H C G F}$

Vậy ta có : ${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$

Câu 28:

Dùng diện tích để chứng tỏ : ${(a - b)}^{2} = a^{2} - 2 a b + b^{2}$ với điều kiện b < a

Dựng hình vuông ABCD có cạnh bằng a

Trên cạnh AB lấy điểm E sao cho BE = b

Từ E dựng đường thẳng song song BC cắt CD tại G

Ta có: CG = b, CE = ( a – b ), GD = ( a – b )

Trên cạnh AD lấy điểm K sao cho AK = b

Từ K kẻ đường thẳng song song với AB cắt BC tại H và cắt EG tại F

Ta có: KD = ( a – b ), BH = b

Hình vuông ABCD có diện tích bằng $a^{2}$

Hình vuông DKFG có diện tích bằng ${(a - b)}^{2}$

Hình chữ nhật AEFK có diện tích bằng ( a – b ) b

Hình vuông EBHF có diện tích bằng $b^{2}$

Hình chữ nhật HCGF có diện tích bằng ( a – b ).b

$S_{A B C D} = S_{D K F G} + S_{A E F K} = S_{E B H F} + S_{H C G F}$

nên ${(a - b)}^{2} + (a - b) b + (a - b) b + b^{2} = a^{2}$

⇒ ${(a - b)}^{2} = a^{2} - 2 a b + b^{2}$

Câu 29:

Đố vui: Có thể dùng kéo cắt một lần và chỉ cắt theo đường thẳng, chia một hình chữ nhật thành hai mảnh để ghép lại được một tam giác vuông hay không ?

Ta có thể cắt ghép như hình vẽ bên.

Câu 30:

Đố vui: Có thể dùng kéo cắt hai lần và chỉ cắt theo đường thằng, chai một hình chữ nhật thành ba mảnh để ghép lại được một tam giác thường hay không ?

Ta có thể cắt ghép như hình bên dưới.

Bắt đầu thi ngay

Bài thi liên quan