18 câu hỏi trắc nghiệm thuộc Bài 11: Toán 8 Hình thoi

Câu 1:

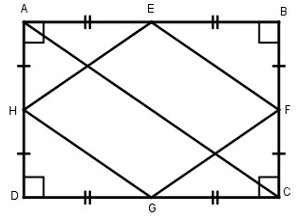
Chứng minh rằng trung điểm bốn cạnh của một hình chữ nhật là một hình thoi.

Xem đáp án

Gọi E, F, G, H lần lượt là trung điểm của các cạnh AB, BC, CD, DA của hình chữ nhật ABCD.

Kẻ đường chéo AC, BD

* Trong $∆$ ABC, ta có:

E là trung điểm của AB

F là trung điểm của BC

Nên EF là đường trung bình của $∆$ ABC.

⇒ EF // AC và EF = 1/2 AC (t/chất đường trung bình của tam giác) (1)

Trong $∆$ ADC, ta có: H là trung điểm của AD

G là trung điểm của DC

Nên HG là đường trung bình của tam giác ADC.

⇒ HG // AC và HG = 1/2 AC (t/chất đường trung bình của tam giác) (2)

Từ (1) và (2) suy ra: EF // HG và EF = HG

Suy ra tứ giác EFGH là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau)

Xét $∆$ AEH và $∆$ DGH, ta có: AH = HD (gt)

$∠$ EAH và $∠$ GDH = $90 °$

AE = DG (vì AB = CD)

Suy ra: $∆$ AEH = $∆$ DGH (c.g.c) ⇒ HE = HG

Vậy hình bình hành EFGH là hình thoi (hình bình hành có 2 cạnh kề bằng nhau).

Câu 2:

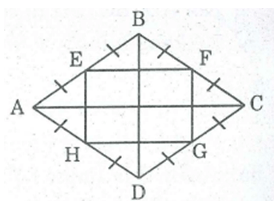
Chứng minh rằng trung điểm các cạnh của một hình thoi là đỉnh của một hình chữ nhật.

Xem đáp án

Giả sử hình thoi ABCD. Gọi E, F, G, H lần lượt là trung điểm của các cạnh AB, BC, CD, DA.

* Trong $∆$ ABC, ta có:

E là trung điểm của AB

F là trung điểm của BC

Nên EF là đường trung bình của $∆$ ABC.

⇒ EF // AC và EF = 1/2 AC (t/chất đường trung bình của tam giác) (1)

* Trong $∆$ ADC, ta có: H là trung điểm của AD

G là trung điểm của CD

Nên HG là đường trung bình của tam giác ADC

⇒ HG // AC và HG = 1/2 AC (t/chất đường trung bình của tam giác) (2)

Từ (1) và (2) suy ra: EF // HG và EF = HG

Suy ra tứ giác EFGH là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau)

Mặt khác: AC ⊥ BD (tính chất hình thoi)

EF // AC (chứng minh trên)

Câu 3:

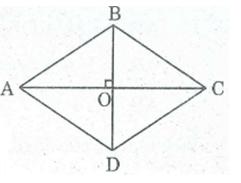
Chứng minh rằng trong hình thoi: Giao điểm của hai đường thẳng chéo là tâm đối xứng của hình thoi.

Xem đáp án

Hình bình hành có tâm đối xứng là giao điểm của hai đường chéo. Hình thoi cũng là một hình bình hành nên cũng có tâm đối xứng là giao điểm hai đường chéo của nó.

Câu 4:

Chứng minh rằng trong hình thoi: Hai đường chéo là hai trục đối xứng của hình thoi.

Xem đáp án

* Ta có: AC ⊥ BD (tính chất hình thoi)

OB = OD (tính chất hình thoi)

Nên AC là đường trung trực của BD.

Do đó điểm đối xứng với điểm B qua AC là D;

Điểm đối xứng với điểm D qua AC là B

Điểm đối xứng với điểm A qua AC là điểm A;

Điểm đối xứng với điểm C qua AC là điểm C

Vậy điểm đối xứng với mỗi đỉnh của hình thoi qua AC cũng thuộc hình thoi

Do đó AC là trục đối xứng của hình thoi ABCD.

* Ta có : OC = OA và AC ⊥ BD (tính chất hình thoi)

Nên BD là đường trung trực của AC

Do đó điểm đối xứng với điểm A qua BD là điểm C

Điểm đối xứng với điểm C qua BD là điểm A

Điểm đối xứng với điểm B qua BD là điểm B

Điểm đối xứng với điểm D qua BD là điểm D

Vậy điểm đối xứng với mỗi đỉnh của hình thoi qua BD cũng thuộc hình thoi.

Do đó BD là trục đối xứng của hình thoi ABCD.

Câu 5:

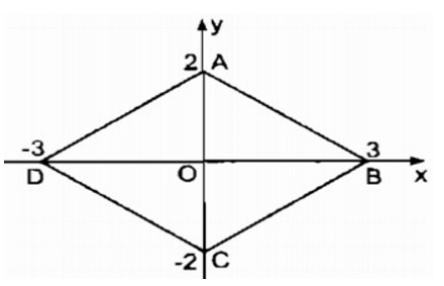
Tứ giác ABCD có tọa độ các đỉnh như sau A(0;2); B(3; 0); C(0;-2) ; D(-3;0).Tứ giác ABCD là hình gì ? Tính chu vi của tứ giác đó.

Xem đáp án

Ta có: A(0;2) và C(0;-2) là hai điểm đối xứng qua O(0;0)

⇒ OA = OC

B(3;0) và D(-3; 0) là hai điểm đối xứng qua O(0;0)

⇒ OB = OD

Tứ giác ABCD là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm của mỗi đường)

Lại có: Ox ⊥ Oy hay AC ⊥ BD.

Vậy tứ giác ABCD là hình thoi

Trong $∆$ OAB vuông tại O, theo định lý Pi-ta-go ta có:

$A B^{2} = O A^{2} + O B^{2}$

$A B^{2} = 2^{2} + 3^{2}$ = 4 + 9 = 13

AB = $\sqrt{13}$

Vậy chu vi của hình thoi bằng 4 $\sqrt{13}$

Câu 6:

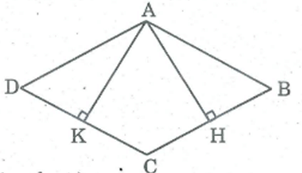
Cho hình thoi ABCD, kẻ đường cao AH, AK. Chứng minh rằng AH =AK.

Xem đáp án

Xét hai tam giác vuông AHB và AKD, ta có:

$∠$ (AHB) = $∠$ (AKD) = $90^{0}$

AB = AD (gt)

$∠$ B = $∠$ D (tính chất hình thoi)

Suy ra: $∆$ AHB = $∆$ AKD (cạnh huyền, góc nhọn)

⇒ AH = AK

Câu 7:

Hình bình hành ABCD có hai đường cao AH, AK bằng nhau. Chứng minh rằng ABCD là hình thoi

Xem đáp án

Xét hai tam giác vuông AHC và AKC, ta có:

$∠$ (AHC) = $∠$ (AKC) = $90^{0}$

AH = AK (gt)

AC cạnh huyền chung

Suy ra: $∆$ AHC = $∆$ AKC (cạnh huyền- cạnh góc vuông)

⇒ $∠$ (ACH) = $∠$ (ACK) hay $∠$ (ACB) = $∠$ (ACD)

⇒ CA là tia phân giác $∠$ (BCD)

Hình bình hành ABCD có đường chéo CA là đường phân giác nên là hình thoi.

Câu 8:

Hình thoi ABCD có $∠$ A = $60^{0}$ . Kẻ hai đường cao BE, BF. Tam giác BEF là tam giác gì? Vì sao?

Xem đáp án

Xét hai tam giác vuông BEA và BFC, ta có:

$∠$ (BEA) = $∠$ (BFC) = $90^{0}$

$∠$ A = $∠$ C (tính chất hình thoi)

BA = BC (gt)

Suy ra: $∆$ BEA = $∆$ BFC (cạnh huyền, góc nhọn)

Do đó, ta có:

* BE = BF ⇒ ΔBEF cân tại B

* $∠$ $B_{1}$ = $∠$ $B_{2}$

Trong tam giác vuông BEA, ta có:

$∠$ A + $∠$ B1= $90^{0}$ ⇒ $∠$ B1= $90^{0}$ – $∠$ A = $90^{0} - 60^{0} = 30^{0}$

⇒ $∠$ $B_{2}$ = $∠$ $B_{1}$ = $30^{0}$

$∠$ A + $∠$ (ABC) = $180^{0}$ (hai góc trong cùng phía bù nhau)

⇒ $∠$ (ABC) = $180^{0}$ – $∠$ A = $180^{0} - 60^{0} = 120^{0}$

⇒ $∠$ (ABC) = $∠$ $B_{1}$ + $∠$ $B_{2}$ + $∠$ $B_{3}$

⇒ $∠$ $B_{3}$ = $∠$ (ABC) – ( $∠$ $B_{1}$ + $∠$ $B_{2}$ ) = $120^{0} - (30^{0} + 30^{0}) = 60^{0}$

Tam giác BEF cân tại B có $∠$ (EBF) = $60^{0}$ nên $∆$ BEF đều.

Câu 9:

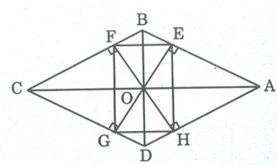
Cho hình thoi ABCD, O là giao điểm của hai đường chéo. Gọi E, F, G, H theo thứ tự là chân Các đường vuông góc kẻ từ O đến AB, BC, CD, DA. Tứ giác EFGH là hình gì? Vì sao?

Xem đáp án

Ta có: AB // CD (gt)

OE ⊥ AB (gt)

⇒ OE ⊥CD

OG ⊥CD(gt)

Suy ra OE trùng với OG nên ba điểm O,E,G thẳng hàng.

BC // AD (gt)

OF ⊥ BC (gt)

⇒ OF ⊥ AD

OH ⊥ AD (gt)

Suy ra OF trùng với OH nên ba điểm O,H,F thẳng hàng.

Vì AC và BD là đường phân giác các góc của hình thoi nên:

OE = OF ( t/chất tia phân giác) (1)

OE = OH ( t/chất tia phân giác) (2)

OH = OG ( t/chất tia phân giác) (3)

Tứ giác EFGH có hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường nên nó là hình chữ nhật.

Câu 10:

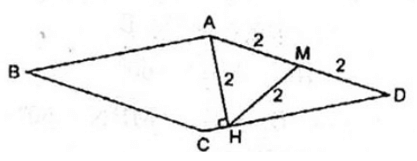
Hình thoi ABCD có chu vi bằng 16cm, đường cao AH = 2cm. Tính các góc của hình thoi, biết $∠$ A > $∠$ B

Xem đáp án

Chu vi hình thoi bằng 16(cm) nên độ dài một cạnh bằng:

16 : 4 = 4(cm)

Gọi M là trung điểm của AD.

*Trong tam giác vuông AHD ta có HM là trung tuyến thuộc cạnh huyền, suy ra: HM = AM = 1/2 AD = 1/2 . 4 = 2(cm)

⇒ AM = HM = AH = 2cm

⇒ $∆$ AHM đều

⇒ $∠$ (HAM ) = $60^{0}$

*Trong tam giác vuông AHD, ta có:

$∠$ (HAD) + $∠$ D = $90^{0}$

⇒ $∠$ D = $90^{0}$ - $∠$ (HAD) = $90^{0}$ – $60^{0}$ = $30^{0}$

⇒ $∠$ B = $∠$ D = $30^{0}$ ( t/chất hình thoi)

$∠$ B + $∠$ C = $180^{0}$ ( hai góc trong cùng phía bù nhau)

⇒ $∠$ C = $180^{0}$ - $∠$ B = $180^{0}$ – $30^{0}$ = $150^{0}$

⇒ $∠$ A = $∠$ C = $150^{0}$ ( tính chất hình thoi).

Câu 11:

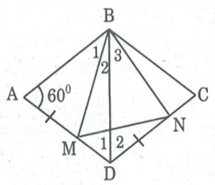
Hình thoi ABCD có góc A = 60°. Trên cạnh AD lấy điểm M, trên cạnh CD lấy điểm N sao cho AM = DN. Tam giác BMN là tam giác gì? Vì sao?

Xem đáp án

Nối BD, ta có AB = AD (gt)

Suy ra $∆$ ABD cân tại A

Mà $∠$ A = $60^{0}$ ⇒ $∆$ ABD đều

⇒ $∠$ (ABD) = $∠$ $D_{1}$ = $60^{0}$ và BD = AB

Suy ra: BD = BC = CD

⇒ $∆$ CBD đều ⇒ $∠$ $D_{2}$ = $60^{0}$

Xét $∆$ BAM và $∆$ BDN,ta có:

AB = BD ( chứng minh trên)

$∠$ A = $∠$ $D_{2}$ = $60^{0}$

AM = DN (giả thiết)

Do đó $∆$ BAM = $∆$ BDN ( c.g.c) ⇒ $∠$ $B_{1}$ = $∠$ $B_{3}$ và BM = BN

Suy ra ΔBMN cân tại B.

Mà $∠$ $B_{2}$ + $∠$ $B_{1}$ = $∠$ (ABD) = $60^{0}$

Suy ra: $∠$ $B_{2}$ + $∠$ $B_{3}$ = $∠$ $B_{2}$ + $∠$ $B_{1}$ = 60° hay $∠$ (MBN) = $60^{0}$

Vậy $∆$ BMN đều

Câu 12:

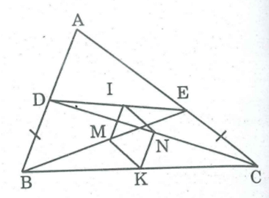
Cho tam giác ABC. Lấy các điểm D,E theo thứ tự trên cạnh AB, AC sao cho BD = CE. Gọi M,N,I,K theo thứ tự là trung điểm của BE, CD, DE, BC. Chứng minh rằng IK vuông góc với MN.

Xem đáp án

*Trong $∆$ BCD,ta có:

K là trung điểm của BC (gt)

N là trung điểm của CD (gt)

Nên NK là đường trung bình của $∆$ BCD

⇒ NK // BD và NK = 1/2 BD (1)

*Trong $∆$ BED,ta có:

M là trung điểm của BE (gt)

I là trung điểm của DE (gt)

Nên MI là đường trung bình của $∆$ BED

⇒ MI // BD và MI = 1/2 BD (t/chất đường trung bình trong tam giác) (2)

Từ (1) và (2) suy ra: MI // NK và MI = NK

Nên tứ giác MKNI là hình bình hành.

*Trong $∆$ BEC ta có MK là đường trung bình.

⇒ MK = 1/2 CE (t/chất đường trung bình của tam giác)

BD = CE (gt). Suy ra: MK = KN

Vậy hình bình hành MKNI là hình thoi.

⇒IK ⊥ MN (t/chất hình thoi).

Câu 13:

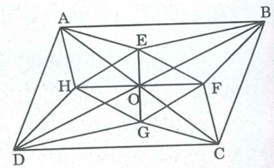
Cho hình bình hành ABCD, các đường chéo cắt nhau tại O. Gọi E,F,G,H theo thứ tự là giao điểm của các đường phân giác của tam giác AOB, BOC, COD, DOA. Chứng minh rằng EFGH là hình thoi.

Xem đáp án

Ta có: $∠$ (AOB) = $∠$ (COD) (đối đỉnh)

$∠$ (EOB ) = 1/2 $∠$ (AOB) (gt)

$∠$ (COG) = 1/2 $∠$ (COD) (gt)

Suy ra: $∠$ (EOB ) = $∠$ (COG)

$∠$ (EOB) + $∠$ (BOC) + $∠$ (COG) = 2 $∠$ (EOB) + $∠$ (BOC)

Mà $∠$ (AOB ) + $∠$ (BOC) = $180^{0}$ ( kề bù).Hay 2 $∠$ (EOB) + $∠$ (BOC ) = $180^{0}$

Suy ra: E,O,G thẳng hàng

Ta lại có: $∠$ (BOC) = $∠$ (AOD ) ( đối đỉnh)

$∠$ (HOD) = 1/2 $∠$ (AOD) (gt)

$∠$ (FOC) = 1/2 $∠$ (BOC) (gt)

Suy ra: $∠$ (HOD) = $∠$ (FOC)

$∠$ (HOD) + $∠$ (COD ) + $∠$ (FOC) = 2 $∠$ (HOD) + $∠$ (COD)

Mà $∠$ (AOD) + $∠$ (COD) = $180^{0}$ ( kề bù). Hay 2 $∠$ (HOD) + $∠$ (COD) = $180^{0}$

Suy ra: H, O, F thẳng hàng

$∠$ (ADO) = $∠$ (CBO) ( so le trong)

$∠$ (HDO) = $∠$ (FBO) ( chứng minh trên)

OD = OB ( t/chất hình bình hành)

$∠$ (HOD) = $∠$ (FOB ) ( đối đỉnh)

Do đó: $∆$ BFO = $∆$ DHO (g.c.g)

⇒ OF = OH

$∠$ (OAB) = $∠$ (OCD) ( so le trong)

$∠$ (OAE) = 1/2 $∠$ (OAB ) (gt)

$∠$ (OCG) = 1/2 $∠$ (OCD) (gt)

Suy ra: $∠$ (OAE) = $∠$ (OCG)

Xét $∆$ OAE và $∆$ OCG,ta có :

$∠$ (OAE) = $∠$ (OCG) ( chứng mình trên)

OA = OC ( t/chất hình bình hành)

$∠$ (EOA) = $∠$ (GOC) ( đối đỉnh)

Do đó: $∆$ OAE= $∆$ OCG (g.c.g) ⇒ OE = OG

Suy ra tứ giác EFGH là hình bình hành ( vì có 2 đường chéo cắt nhau tại trung điểm của mỗi đường)

OE ⊥ OF (tính chất tia phân giác của hai góc kề bù) hay EG ⊥ FH

Vậy tứ giác EFGH là hình thoi

Câu 14:

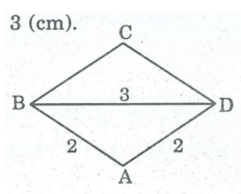
Dựng hình thoi ABCD biết cạnh bằng 2cm, một đường chéo bằng 3cm.

Xem đáp án

*Cách dựng:

- Dựng $∆$ ABD biết AB = AD = 2(cm), BD = 3(cm).

- Trên nửa mặt phẳng bờ BD không chứa điểm A. Từ B dựng tia Bx // AD, từ D dựng tia DY // AB, chúng cắt nhau tại C.

Ta có hình thoi ABCD cần dựng

*Chứng minh:

Vì AB // CD và AD // BC nên tứ giác ABCD là hình bình hành

AB = AD = 2cm. Vậy tứ giác ABCD là hình thoi.

Lại có: BD = 3cm

Hình thoi dựng được thỏa mãn điều kiện bài toán.

Câu 15:

Cạnh của một hình thoi bằng 25, một đường chéo bằng 14. Đường chéo kia bằng:

A. 24

B. 48

C. $\sqrt{429}$

D. Một đáp số khác.

Hãy chọn phương án đúng

Xem đáp án

Chọn B: 48 đúng

Câu 16:

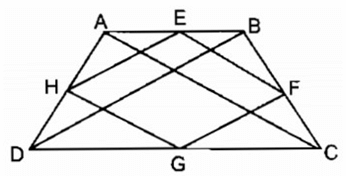
Cho hình thang cân ABCD( AB // CD). Gọi E, F, G, H theo thứ tự là trung điểm của các cạnh AB, BC, CD, DA. Tứ giác EFGH là hình gì ?

Xem đáp án

Trong $∆$ ABD ta có:

E là trung điểm của AB (gt)

H là trung điểm của AD (gt)

nên EH là đường trung bình của $∆$ ABD

⇒ EH // BD và EH = 1/2 BD (tính chất đường trung bình của tam giác) (1)

- Trong $∆$ CBD ta có:

F là trung điểm của BC (gt)

G là trung điểm của CD (gt)

nên FG là đường trung bình của $∆$ CBD

⇒ FG // BD và FG = 1/2 BD (tính chất đường trung bình của tam giác) (2)

Từ (1) và (2) suy ra: EH // FG và EH = FG

Suy ra: Tứ giác EFGH là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau)

Trong $∆$ ABC ta có:

EF là đường trung bình

⇒ EF = 1/2 AC (tính chất đường trung bình của tam giác) (3)

AC = BD (tính chất hình thang cân) (4)

Từ (1), (3) và (4) suy ra: EH = EF

Vậy : Tứ giác EFGH là hình thoi.

Câu 17:

Cho tam giác ABC, điểm D thuộc cạnh BC. Qua D kẻ đường thẳng song song với AC, cắt AB ở I. Qua D kẻ đường thẳng song song với AB, cắt AC ở K. Tứ giác AIDK là hình gì ?

Xem đáp án

Ta có: DK // AB (gt)

hay DK // AI

DI // AC (gt)

hay DI // AK

Vậy tứ giác AIDK là hình bình hành

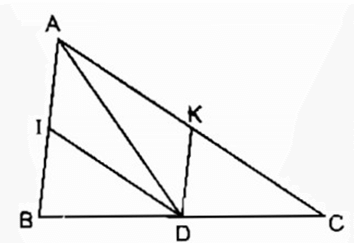
Câu 18:

Cho tam giác ABC, điểm D thuộc cạnh BC. Qua D kẻ đường thẳng song song với AC, cắt AB ở I. Qua D kẻ đường thẳng song song với AB, cắt AC ở K. Điểm D ở vị trí nào trên cạnh BC thì AIDK là hình thoi ?

Xem đáp án

Để hình bình hành AIDK là hình thoi.

⇒ AD là đường phân giác của $∠$ (IAK)

hay AD là đường phân giác của $∠$ (BAC)

Ngược lại nếu AD là tia phân giác của $∠$ (BAC)

Ta có tứ giác AIDK là hình bình hành có đường chéo AD là phân giác của góc A nên tứ giác AIDK là hình thoi

Vậy hình bình hành AIDK là hình thoi khi và chỉ khi D là giao điểm tia phân giác của góc A và cạnh BC.

CHỌN BỘ SÁCH BẠN MUỐN XEM

Giải Sách Bài Tập Toán 8 Tập 1

Bài 11: Toán 8 Hình thoi

Danh sách câu hỏi

Bài thi liên quan